Table of Contents
Problem Statement
Given a Binary Search Tree(BST), write an algorithm to convert the BST to a Balanced Binary Search Tree. A balanced Binary Search tree is nothing but a binary search tree whose difference between the height of left subtree and right subtree is less than or equal to 1.
Examples
Input

Output
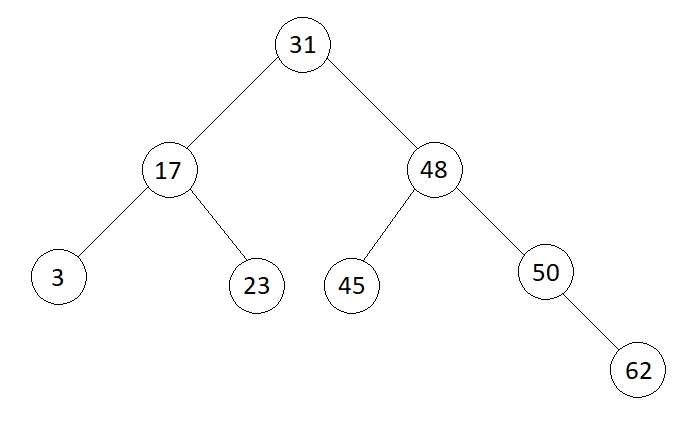
Pre-order : 31 17 3 23 48 45 50 62
Input
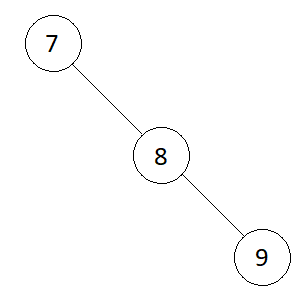
Output
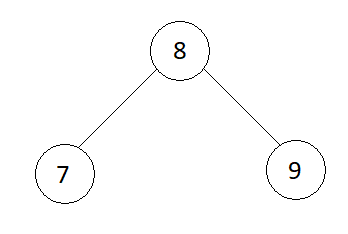
Preorder: 8 7 9
Algorithm for converting a normal BST to balanced BST
One approach could be to traverse the given binary search tree in in-order fashion and store the elements in a self-balancing tree, like an AVL tree or a red-black tree. This approach is not much efficient, it takes O(N log N) time and uses O(N) extra space.
The given problem is similar to building a balanced binary search tree from a sorted array and we know how to convert a sorted array or list to a balanced binary search tree. If we take a look closer to the given problem, we can convert the problem to constructing a balanced binary search tree from a sorted array.
The idea is to traverse the given BST in in-order traversal and store the nodes in an array. The array will contain the data in sorted order. Then we convert the sorted array into a balanced binary search tree.
1. Traverse the given binary search tree in in-order traversal and store the nodes in an array, let the array be inOrderNodes. 2. The middle element of the array forms the root of the balanced BST and all the elements to the left of middle element forms the left sub-tree and all the elements to the right of middle element forms the right sub-tree. 3. Make root's left as the result of a recursive call for step 2. For left sub-tree the start index is start in step 2 and end index is mid - 1. 4. Make root's right as the result of a recursive call for step 2. For right sub-tree the start index is mid + 1 and end index is end in step 2. 5. Return root.
Complexity Analysis
Time Complexity = O(n), since we traverse the whole tree having n nodes. We have linear time complexity for this algorithm.
Space Complexity = O(n), because we are using an array of size n for storing the inorder traversal of the binary search tree.
where n is the number of nodes in the given binary search tree.
JAVA Code for converting a normal BST to balanced BST
/* package whatever; // don't place package name! */
import java.util.*;
import java.lang.*;
import java.io.*;
import java.util.ArrayList;
class ConvertANormalBSTToBalancedBST {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// function to print pre-order traversal of a binary tree
private static void preOrder(Node root) {
if (root != null) {
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
}
// function to store the in-order traversal of a binary tree to an array
private static void storeInOrderTraversal(Node root, ArrayList<Integer> inOrderNodes) {
if (root != null) {
storeInOrderTraversal(root.left, inOrderNodes);
inOrderNodes.add(root.data);
storeInOrderTraversal(root.right, inOrderNodes);
}
}
private static Node convertSortedArrayToBalancedBST(ArrayList<Integer> inOrderNodes, int start, int end) {
// Base Case
if (start > end) {
return null;
}
// middle element of the array forms the node
int mid = (start + end) / 2;
Node root = new Node(inOrderNodes.get(mid));
// elements to the left of middle element forms left subtree
root.left = convertSortedArrayToBalancedBST(inOrderNodes, start, mid - 1);
// elements to the right of middle element forms right subtree
root.right = convertSortedArrayToBalancedBST(inOrderNodes, mid + 1, end);
// return root
return root;
}
private static Node convertToBalancedBST(Node root) {
// create an array
ArrayList<Integer> inOrderNodes = new ArrayList<>();
// store the in-order traversal in the array
storeInOrderTraversal(root, inOrderNodes);
// make balanced BST from sorted array
return convertSortedArrayToBalancedBST(inOrderNodes, 0, inOrderNodes.size() - 1);
}
public static void main(String[] args) {
// Example 1
Node root1 = new Node(50);
root1.left = new Node(23);
root1.right = new Node(62);
root1.left.left = new Node(17);
root1.left.right = new Node(45);
root1.left.left.left = new Node(3);
root1.left.right.left = new Node(31);
root1.left.right.right = new Node(48);
root1 = convertToBalancedBST(root1);
preOrder(root1);
System.out.println();
// Example 2
Node root2 = new Node(7);
root2.right = new Node(8);
root2.right.right = new Node(9);
root2 = convertToBalancedBST(root2);
preOrder(root2);
System.out.println();
}
}31 17 3 23 48 45 50 62 8 7 9
C++ Code for converting a normal BST to balanced BST
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to print pre-order traversal of a binary tree
void preOrder(Node *root) {
if (root != NULL) {
cout<<root->data<<" ";
preOrder(root->left);
preOrder(root->right);
}
}
// function to store the in-order traversal of a binary tree to an array
void storeInOrderTraversal(Node *root, vector<int> &inOrderNodes) {
if (root != NULL) {
storeInOrderTraversal(root->left, inOrderNodes);
inOrderNodes.push_back(root->data);
storeInOrderTraversal(root->right, inOrderNodes);
}
}
Node* convertSortedArrayToBalancedBST(vector<int> &inOrderNodes, int start, int end) {
// Base Case
if (start > end) {
return NULL;
}
// middle element of the array forms the node
int mid = (start + end) / 2;
Node *root = new Node(inOrderNodes[mid]);
// elements to the left of middle element forms left subtree
root->left = convertSortedArrayToBalancedBST(inOrderNodes, start, mid - 1);
// elements to the right of middle element forms right subtree
root->right = convertSortedArrayToBalancedBST(inOrderNodes, mid + 1, end);
// return root
return root;
}
Node* convertToBalancedBST(Node *root) {
// create an array
vector<int> inOrderNodes;
// store the in-order traversal in the array
storeInOrderTraversal(root, inOrderNodes);
// make balanced BST from sorted array
return convertSortedArrayToBalancedBST(inOrderNodes, 0, inOrderNodes.size() - 1);
}
int main() {
// Example 1
Node *root1 = new Node(50);
root1->left = new Node(23);
root1->right = new Node(62);
root1->left->left = new Node(17);
root1->left->right = new Node(45);
root1->left->left->left = new Node(3);
root1->left->right->left = new Node(31);
root1->left->right->right = new Node(48);
root1 = convertToBalancedBST(root1);
preOrder(root1);
cout<<endl;
// Example 2
Node *root2 = new Node(7);
root2->right = new Node(8);
root2->right->right = new Node(9);
root2 = convertToBalancedBST(root2);
preOrder(root2);
cout<<endl;
return 0;
}31 17 3 23 48 45 50 62 8 7 9