Table of Contents
Problem Statement
The problem “Level order traversal using two Queues” states that you are given a binary tree, print its level order traversal line by line.
Examples
Input
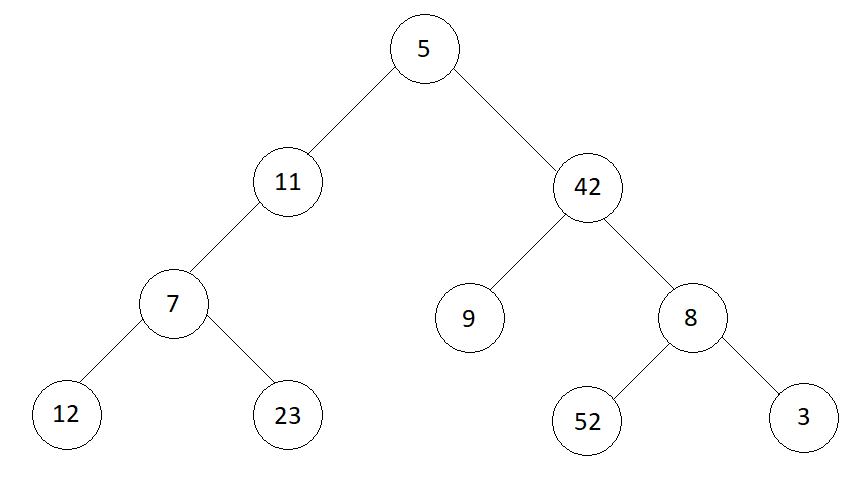
5 11 42 7 9 8 12 23 52 3
Input

1 2 3 4 5 6
Algorithm for Level Order Traversal Using Two Queues
To print the level order traversal using two queues, we first push the first level(root) to first queue, while popping out a level from first queue, we push the next level into second queue and while popping out a level from second queue, push the next level to first queue. Repeat this process till either of the two queues is not empty.
- Create two queues q1 and q2.
- Push the root to q1.
- While either q1 is not empty or q2 is not empty repeat step 4 and 5.
- While q1 is not empty, one by one remove elements from queue, print it and push its children to q2. Print a new line after the queue becomes empty.
- While q2 is not empty, one by one remove elements from queue, print it and push its children to q1. Print a new line after the queue becomes empty.
Explanation
Consider the tree in second example above.
Step 1
Create two queues q1 and q2.
q1 = null and q2 = null
Step 2
Push the root to queue q1
q1 = 1 and q2 = null
Step 3
Repeat step 4 and 5 while either of queues q1 or q2 is not empty
Step 4 and 5
q1 = 2 and q2 = null
Iteration 1
Print 2.
q1 = null and q2 = 2 -> 3
Print line break.
Iteration 2
Print 2 and 3.
q1 = 4 -> 5 -> 6 and q2 = null
Print line break.
Iteration 3
Print 4, 5 and 6.
q1 = null and q2 = null
Print line break.
As both the queues become empty, so we stop here.
Code
Java Code for Level Order Traversal Using Two Queues
import java.util.LinkedList;
import java.util.Queue;
class LevelOrderTraversalUsingTwoQueues {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
private static void levelOrderTraversal(Node root) {
if (root == null) {
System.out.println();
return;
}
// create two queues q1 and q2
Queue<Node> q1 = new LinkedList<>();
Queue<Node> q2 = new LinkedList<>();
// push the root to queue q1
q1.add(root);
// while either q1 is not empty or q2 is not empty
while (!q1.isEmpty() || !q2.isEmpty()) {
// Pop out a level from q1, print it and push next level to q2
while (!q1.isEmpty()) {
// remove a node from q1
Node curr = q1.poll();
// print the node
System.out.print(curr.data + " ");
// add its children to queue q2
if (curr.left != null)
q2.add(curr.left);
if (curr.right != null)
q2.add(curr.right);
}
// print line break
System.out.println();
// Pop out a level from queue q2 and push next level to q1
while (!q2.isEmpty()) {
// remove a node from q2
Node curr = q2.poll();
// print the node
System.out.print(curr.data + " ");
// add its children to queue q2
if (curr.left != null)
q1.add(curr.left);
if (curr.right != null)
q1.add(curr.right);
}
// print line break
System.out.println();
}
System.out.println();
}
public static void main(String[] args) {
// Example Tree 1
Node root1 = new Node(5);
root1.left = new Node(11);
root1.right = new Node(42);
root1.left.left = new Node(7);
root1.right.left = new Node(9);
root1.right.right = new Node(8);
root1.left.left.left = new Node(12);
root1.left.left.right = new Node(23);
root1.right.right.left = new Node(52);
root1.right.right.right = new Node(3);
levelOrderTraversal(root1);
// Example Tree 2
Node root2 = new Node(1);
root2.left = new Node(2);
root2.right = new Node(3);
root2.left.left = new Node(4);
root2.left.right = new Node(5);
root2.right.right = new Node(6);
levelOrderTraversal(root2);
}
}5 11 42 7 9 8 12 23 52 3 1 2 3 4 5 6
C++ Code for Level Order Traversal Using Two Queues
#include<bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to create a new node
Node* newNode(int d) {
Node *node = new Node(d);
return node;
}
void levelOrderTraversal(Node *root) {
if (root == NULL) {
cout<<endl;
return;
}
// create two queues q1 and q2
queue<Node *> q1;
queue<Node *> q2;
// push the root to queue q1
q1.push(root);
// while either q1 is not empty or q2 is not empty
while (!q1.empty() || !q2.empty()) {
// Pop out a level from q1, print it and push next level to q2
while (!q1.empty()) {
// remove a node from q1
Node *curr = q1.front();
q1.pop();
// print the node
cout<<curr->data<<" ";
// add its children to queue q2
if (curr->left != NULL)
q2.push(curr->left);
if (curr->right != NULL)
q2.push(curr->right);
}
// print line break
cout<<endl;
// Pop out a level from queue q2 and push next level to q1
while (!q2.empty()) {
// remove a node from q2
Node *curr = q2.front();
q2.pop();
// print the node
cout<<curr->data<<" ";
// add its children to queue q2
if (curr->left != NULL)
q1.push(curr->left);
if (curr->right != NULL)
q1.push(curr->right);
}
// print line break
cout<<endl;
}
cout<<endl;
}
int main() {
// Example Tree 1
Node *root1 = newNode(5);
root1->left = newNode(11);
root1->right = newNode(42);
root1->left->left = newNode(7);
root1->right->left = newNode(9);
root1->right->right = newNode(8);
root1->left->left->left = newNode(12);
root1->left->left->right = newNode(23);
root1->right->right->left = newNode(52);
root1->right->right->right = newNode(3);
levelOrderTraversal(root1);
// Example Tree 2
Node *root2 = newNode(1);
root2->left = newNode(2);
root2->right = newNode(3);
root2->left->left = newNode(4);
root2->left->right = newNode(5);
root2->right->right = newNode(6);
levelOrderTraversal(root2);
return 0;
}5 11 42 7 9 8 12 23 52 3 1 2 3 4 5 6
Complexity Analysis
Time Complexity
O(N), since we have traversed over all the nodes in tree. Thus the time complexity is linear.
Space Complexity
O(N), as we have traversed over the nodes in the tree. We were also inserting them in the queues and thus the space complexity is also linear.