Table of Contents
Problem Statement
The problem “Priority Queue using doubly linked list” asks to implement the following functions of priority queue using doubly linked list.
- push(x, p) : Enqueue an element x with priority p in the priority queue at appropriate position.
- pop() : Remove and return the element with highest priority in the priority queue.
- peek() : Return the element with highest priority in the priority queue without removing it.
Example
push(5, 2) push(1, 3) peek() push(7, 5) push(9, 1) pop() pop() peek()
1 7 1 5
Algorithm to implement Priority Queue using doubly linked list
Priority Queue using doubly linked list is implemented in the same way as priority queue using singly linked list. Here in doubly linked list we have to modify some extra pointers during insertion and deletion.
The idea is same, to maintain the doubly linked list in decreasing order of priority, so that the highest priority element is always at the front.
push(x, p)
To Push an element x with priority p into the priority queue, find the appropriate place for the element, and insert it. The appropriate place is just before the first element with a priority less than p.
For example,
priorityQueue = (7, 5) -> (9, 4) -> (8, 2)
Push(6, 3)
The appropriate place for (6, 3) is just before (8, 2), queue after insertion is,
priorityQueue = (7, 5) -> (9, 4) -> (6, 3) -> (8, 2)
See the image below for clarification.
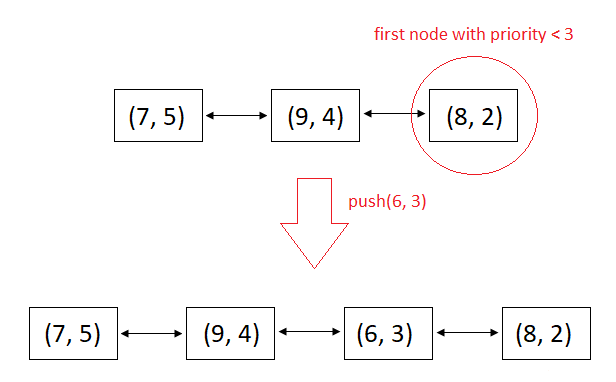
- Traverse in the priority queue starting from head and find the first node with priority less than p.
- One of the three cases is possible.
- There is no element with priority less than p. In such a case insert the new node at the end of the priority queue.
- All the nodes are having priorities less than p. In such a case insert the new node at the beginning of the priority queue.
- There are some nodes with priority less than p and some nodes with priority greater than p. In such a case insert the new node before the first node with priority less than p. This case is shown in the image above.
Time Complexity = O(n)
Space Complexity = O(1)
where n is the total number of nodes in priority queue before insertion.
pop()
The highest priority element is present at the beginning of priority queue. If the priority queue is not empty delete the first element and return it, else it is not possible to pop.
Time Complexity = O(1)
peek()
The highest priority element is present at the beginning of priority queue. If the priority queue is not empty return the value of first element in the priority queue.
Time Complexity = O(1)
Code
Java Code to implement Priority Queue using doubly linked list
class PriorityQueueUsingDoublyLinkedList {
// class representing node of a doubly linked list
static class Node {
int data;
int priority;
Node next, prev;
public Node(int data, int priority) {
this.data = data;
this.priority = priority;
}
}
// head of doubly linked list
private static Node head = null;
private static void push(int data, int priority) {
// if head is null this is the first node to be inserted
// mark head as new Node
if (head == null) {
Node newNode = new Node(data, priority);
head = newNode;
return;
}
// create a new node with specified data
Node node = new Node(data, priority);
// find the first node having priority less than 'priority'
Node temp = head, parent = null;
while (temp != null && temp.priority >= priority) {
parent = temp;
temp = temp.next;
}
// Case 1 : All the nodes are having priorities less than 'priority'
if (parent == null) {
// insert the new node at the beginning of linked list
node.next = head;
head.prev = node;
head = node;
}
// Case 2 : All the nodes are having priorities greater than 'priority'
else if (temp == null) {
// insert the node at the end of the linked list
parent.next = node;
node.prev = parent;
}
// Case 3 : Some nodes have priority higher than 'priority' and
// some have priority lower than 'priority'
else {
// insert the new node before the first node having priority
// less than 'priority'
parent.next = node;
node.prev = parent;
node.next = temp;
temp.prev = node;
}
}
private static int peek() {
// if head is not null, return the element at first position
if (head != null) {
return head.data;
}
return -1;
}
private static int pop() {
// if head is not null, delete the element at first position and return its value
if (head != null) {
int curr = head.data;
head = head.next;
if (head != null) {
head.prev = null;
}
return curr;
}
return -1;
}
public static void main(String[] args) {
// Example
push(5, 2);
push(1, 3);
System.out.println(peek());
push(7, 5);
push(9, 1);
System.out.println(pop());
System.out.println(pop());
System.out.println(peek());
}
}1 7 1 5
C++ code to implement Priority Queue using doubly linked list
#include <bits/stdc++.h>
using namespace std;
// class representing node of a doubly linked list
class Node {
public:
int data, priority;
Node *next;
Node *prev;
Node(int d, int p) {
data = d;
priority = p;
next = prev = NULL;
}
};
// head of doubly linked list
Node *head = NULL;
void push(int data, int priority) {
// if head is null this is the first node to be inserted
// mark head as new Node
if (head == NULL) {
Node *newNode = new Node(data, priority);
head = newNode;
return;
}
// create a new node with specified data
Node *node = new Node(data, priority);
// find the first node having priority less than 'priority'
Node *temp = head;
Node *parent = NULL;
while (temp != NULL && temp->priority >= priority) {
parent = temp;
temp = temp->next;
}
// Case 1 : All the nodes are having priorities less than 'priority'
if (parent == NULL) {
// insert the new node at the beginning of linked list
node->next = head;
head->prev = node;
head = node;
}
// Case 2 : All the nodes are having priorities greater than 'priority'
else if (temp == NULL) {
// insert the node at the end of the linked list
parent->next = node;
node -> prev = parent;
}
// Case 3 : Some nodes have priority higher than 'priority' and
// some have priority lower than 'priority'
else {
// insert the new node before the first node having priority
// less than 'priority'
parent->next = node;
node->prev = parent;
node->next = temp;
temp->prev = node;
}
}
int peek() {
// if head is not null, return the element at first position
if (head != NULL) {
return head->data;
}
return -1;
}
int pop() {
// if head is not null, delete the element at first position and return its value
if (head != NULL) {
int curr = head->data;
head = head->next;
if (head != NULL) {
head->prev = NULL;
}
return curr;
}
return -1;
}
int main() {
// Example
push(5, 2);
push(1, 3);
cout<<peek()<<endl;
push(7, 5);
push(9, 1);
cout<<pop()<<endl;
cout<<pop()<<endl;
cout<<peek()<<endl;
return 0;
}1 7 1 5