In priority queue using a singly linked list problem, we need to implement a priority queue by using a singly linked list. A priority queue contains the following operations,
- push(x, p): Add an element x with priority p at an appropriate position in the priority queue.
- pop(): Remove and return the element with the highest priority
- peek(): Return the element with the highest priority
Table of Contents
Example
Input:
push(5, 2)
push(1, 3)
peek()
push(7, 5)
push(9, 1)
pop()
pop()
peek()
Output:
1
7
1
5
Algorithm for Priority Queue Using Singly Linked List
The idea is to maintain the linked list in descending order of priority so that the highest priority element is at the front.
push(x, p)
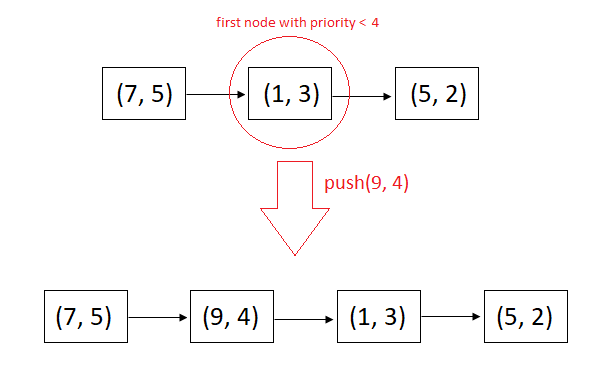
As the elements are arranged in descending order of priorities, so an element with priority p is inserted before the first element with a priority less than p, so that the order of priorities is not disturbed. Three cases arise,
- No element with priority less than p, add the new element at the end of the linked list.
- All the elements have priority less than p, add the new element at the start of the linked list.
- Some elements have priority less than p while others have priority more than p, add the new element before the first element having priority less than p.
Time Complexity = O(n)
Pseudo Code for Priority Queue Using Singly Linked List
- Make a new node with data = x and priority = p, let it be newNode
- If the head is null, this is the first node to be inserted, so make head = newNode and return.
- Create a node temp equals head and a node prev equals null.
- Find the first node with a priority less than p by running a loop while temp is not null and temp’s priority is greater than p. At every iteration, update prev as temp and temp as temp.next.
- After the end of the loop, if the temp is null, it means there is no node with a priority less than p, insert the newNode at the end of the linked list, that is, do prev.next = newNode.
- Else if prev is null, this implies that all the nodes are having priority greater than p. Do newNode.next = head and head = newNode.
- Else, insert the new node before temp, that is, do newNode.next = temp and prev.next = newNode.
pop()
The front of the linked list contains the highest priority element, remove it, and return.
Time Complexity = O(1)
peek()
The front of the linked list contains the highest priority element, return it.
Time Complexity = O(1)
JAVA Code for Priority Queue Using Singly Linked List
public class PriorityQueueUsingSinglyLinkedList {
// class representing node of a linked list
static class Node {
int data;
int priority;
Node next;
public Node(int data, int priority) {
this.data = data;
this.priority = priority;
}
}
// Variable representing the head of linked list
private static Node head = null;
private static void push(int x, int p) {
// Create a new node
Node newNode = new Node(x, p);
// If head is null, this is the first node to be added
// so make head = newNode
if (head == null) {
head = newNode;
return;
}
Node temp = head;
Node prev = null;
// search for first node having priority less than p
while (temp != null && temp.priority > p) {
prev = temp;
temp = temp.next;
}
if (temp == null) {
// no node with priority less than this node (Case 1)
prev.next = newNode;
} else {
if (prev == null) {
// all the nodes have priority less than p (Case 2)
// add this node at the starting
newNode.next = head;
head = newNode;
} else {
// Case 3
// add this node before the node with priority less than p
newNode.next = temp;
prev.next = newNode;
}
}
}
private static int peek() {
// head of the linked list contains the maximum priority element
if (head != null) {
return head.data;
}
return -1;
}
private static int pop() {
// head of the linked list contains the maximum priority element
if (head != null) {
int data = head.data;
// removing the highest priority element
head = head.next;
return data;
}
return -1;
}
public static void main(String[] args) {
// Example
push(5, 2);
push(1, 3);
System.out.println(peek());
push(7, 5);
push(9, 1);
System.out.println(pop());
System.out.println(pop());
System.out.println(peek());
}
}1 7 1 5
C++ Code for Priority Queue Using Singly Linked List
#include<bits/stdc++.h>
using namespace std;
// class representing a tree node
class Node {
public:
int data;
int priority;
Node *next;
Node(int d, int p) {
data = d;
priority = p;
next = NULL;
}
};
// function to create a new node
Node* newNode(int x, int p) {
Node *node = new Node(x, p);
return node;
}
// Variable representing the head of linked list
Node *head = NULL;
void push(int x, int p) {
// Create a new node
Node *node = newNode(x, p);
// If head is null, this is the first node to be added
// so make head = newNode
if (head == NULL) {
head = node;
return;
}
Node *temp = head;
Node *prev = NULL;
// search for first node having priority less than p
while (temp != NULL && temp->priority > p) {
prev = temp;
temp = temp->next;
}
if (temp == NULL) {
// no node with priority less than this node (Case 1)
prev->next = node;
} else {
if (prev == NULL) {
// all the nodes have priority less than p (Case 2)
// add this node at the starting
node->next = head;
head = node;
} else {
// Case 3
// add this node before the node with priority less than p
node->next = temp;
prev->next = node;
}
}
}
int pop() {
// head of the linked list contains the maximum priority element
if (head != NULL) {
int data = head->data;
// removing the highest priority element
head = head->next;
return data;
}
return -1;
}
int peek() {
// head of the linked list contains the maximum priority element
if (head != NULL) {
return head->data;
}
return -1;
}
int main() {
// Example
push(5, 2);
push(1, 3);
cout<<peek()<<endl;
push(7, 5);
push(9, 1);
cout<<pop()<<endl;
cout<<pop()<<endl;
cout<<peek()<<endl;
return 0;
}1 7 1 5