Table of Contents
Problem Statement
The problem “Sum of minimum and maximum elements of all subarrays of size k” states that you are given an array containing positive and negative integers, find the sum of minimum and maximum elements of all the sub-arrays of size k.
Examples
arr[] = {5, 9, 8, 3, -4, 2, 1, -5}
k = 417
Explanation
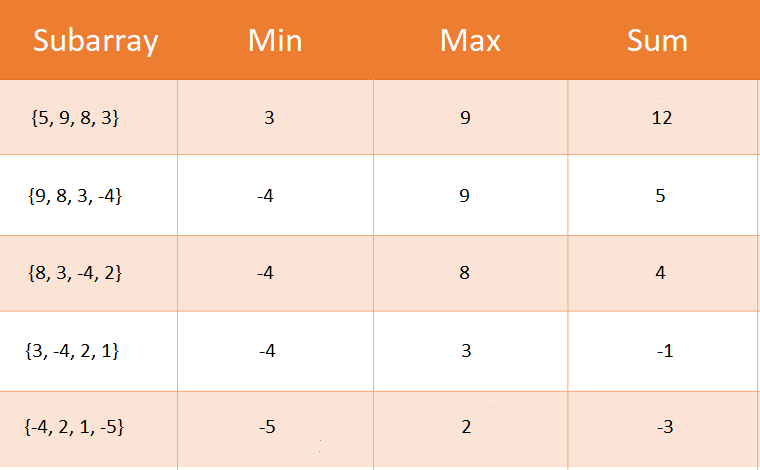
All the sub-arrays of size 4 are,
{5, 9, 8, 3} : min + max = 9 + 3 = 12
{9, 8, 3, -4} : min + max = -4 + 9 = 5
{8, 3, -4, 2} : min + max = -4 + 8 = 4
{3, -4, 2, 1} : min + max = -4 + 3 = -1
{-4, 2, 1, -5} : min + max = -5 + 2 = -3
arr[] = {1, -1, 2, -2, 3, -3}
k = 22
Explanation
All the sub-arrays of size 2 are,
{1, -1} : min + max = -1 + 1 = 0
{-1, 2} : min + max = -1 + 2 = 1
{2, -2} : min + max = -2 + 2 = 0
{-2, 3} : min + max = -2 + 3 = 1
{3, -3} : min + max = -3 + 3 = 0
Approach
Naive Approach
Traverse all the sub-arrays of size k to find their minimum and maximum elements and print the sum.
- Initialize a variable sum as 0.
- Run a loop for i equals 0 to (n – k), where n is the total number of elements in the given array. Each i acts as the starting point of a sub-array of size k.
- Run a nested loop for j = i to (i + k)(not included), this loop represents a sub-array of size k. Traverse this sub-array and find the minimum and maximum elements, let these be min and max respectively.
- Add (min + max) to the sum.
- At the end of the traversal, return sum.
where n is the total number of elements in the given array.
Java Code to find Sum of minimum and maximum elements of all subarrays of size k
class SumOfMinimumAndMaximumElementsOfAllSubarraysOfSizeK {
private static int sumOfMinMax(int[] arr, int k) {
int n = arr.length;
// initialize sum as 0
int sum = 0;
// Traverse all the subarray of size k one by one
for (int i = 0; i <= n - k; i++) {
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
// traverse the current subarray and find the min and max
for (int j = i; j < i + k; j++) {
min = Math.min(min, arr[j]);
max = Math.max(max, arr[j]);
}
// add (min + max) to the sum
sum += (min + max);
}
return sum;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{5, 9, 8, 3, -4, 2, 1, -5};
int k1 = 4;
System.out.println(sumOfMinMax(arr1, k1));
// Example 2
int arr2[] = new int[]{1, -1, 2, -2, 3, -3};
int k2 = 2;
System.out.println(sumOfMinMax(arr2, k2));
}
}17 2
C++ Code to find Sum of minimum and maximum elements of all subarrays of size k
#include<bits/stdc++.h>
using namespace std;
int sumOfMinMax(int *arr, int k, int n) {
// initialize sum as 0
int sum = 0;
// Traverse all the subarray of size k one by one
for (int i = 0; i <= (n - k); i++) {
int min = INT_MAX;
int max = INT_MIN;
// traverse the current subarray and find the min and max
for (int j = i; j < i + k; j++) {
min = std::min(min, arr[j]);
max = std::max(max, arr[j]);
}
// add (min + max) to the sum
sum += (min + max);
}
return sum;
}
int main() {
// Example 1
int arr1[] = {5, 9, 8, 3, -4, 2, 1, -5};
int k1 = 4;
cout<<sumOfMinMax(arr1, k1, sizeof(arr1) / sizeof(arr1[0]))<<endl;
// Example 2
int arr2[] = {1, -1, 2, -2, 3, -3};
int k2 = 2;
cout<<sumOfMinMax(arr2, k2, sizeof(arr2) / sizeof(arr2[0]))<<endl;
return 0;
}17 2
Complexity Analysis
Time Complexity = O(n * k)
Space Complexity = O(1)
Here the time complexity is polynomial because we solving the problem for each sub-array independently. Since we have been storing only;y two variables for maximum and minimum, the space required is constant.
Optimal Approach
Create two Deque d1 and d2, both the deques store the indices of elements that may contribute in the minimum and maximum of a sub-array. Deque d1 contains the elements in decreasing order from front to rear and d2 contains elements in increasing order from front to rear.
- Initialize a variable sum as 0. Create two deques d1 and d2. Consider the first sub-array of size k.
- While the current element of sub-array of size k is greater than or equal to the element at index rear of d1, remove the rear element of Deque d1.
- While the current element of sub-array of size k is smaller than or equal to the element at index rear of d2, remove the rear element of Deque d2.
- Add the current index to the rear of both the deques.
- Rear of deque d1 is the index of maximum element of the sub-array and rear of deque d2 is the index of minimum element of the sub-array. Add the sum of maximum and minimum element to the variable sum.
- Traverse the remaining sub-arrays of size k, and repeat steps 2 to 5. For all the remaining sub-arrays use the sliding window technique and only process the element not present in the previous sub-array.
- After traversing all the sub-arrays, return sum.
Java code to find Sum of minimum and maximum elements of all subarrays of size k
import java.util.Deque;
import java.util.LinkedList;
class SumOfMinimumAndMaximumElementsOfAllSubarraysOfSizeK {
private static int sumOfMinMax(int[] arr, int k) {
int n = arr.length;
// initialize sum as 0
int sum = 0;
// create 2 deques d1 and d2
Deque<Integer> d1 = new LinkedList<>();
Deque<Integer> d2 = new LinkedList<>();
// first subarray
for (int i = 0; i < k; i++) {
// only push the elements that may contribute to maximum
while (!d1.isEmpty() && arr[d1.peekLast()] <= arr[i])
d1.removeLast();
// only push the elements that may contribute to minimum
while (!d2.isEmpty() && arr[d2.peekLast()] >= arr[i])
d2.removeLast();
// add the current elememt's index
d1.addLast(i);
d2.addLast(i);
}
// sum of min and max for first subarray
sum += arr[d2.peekFirst()] + arr[d1.peekFirst()];
// traverse the remaining subarray
for (int i = k; i < n; i++) {
// remove the previous element (sliding window technique)
while (!d2.isEmpty() && d2.peekFirst() <= i - k)
d2.removeFirst();
while (!d1.isEmpty() && d1.peekFirst() <= i - k)
d1.removeFirst();
// only push the elements that may contribute to maximum
while (!d1.isEmpty() && arr[d1.peekLast()] <= arr[i])
d1.removeLast();
// only push the elements that may contribute to minimum
while (!d2.isEmpty() && arr[d2.peekLast()] >= arr[i])
d2.removeLast();
// add the current element's index
d1.addLast(i);
d2.addLast(i);
// sum of min and max for current subarray
sum += arr[d2.peekFirst()] + arr[d1.peekFirst()];
}
// return total sum
return sum;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{5, 9, 8, 3, -4, 2, 1, -5};
int k1 = 4;
System.out.println(sumOfMinMax(arr1, k1));
// Example 2
int arr2[] = new int[]{1, -1, 2, -2, 3, -3};
int k2 = 2;
System.out.println(sumOfMinMax(arr2, k2));
}
}17 2
C++ Code to find Sum of minimum and maximum elements of all subarrays of size k
#include<bits/stdc++.h>
using namespace std;
int sumOfMinMax(int *arr, int k, int n) {
// initialize sum as 0
int sum = 0;
// create 2 deques d1 and d2
deque<int> d1;
deque<int> d2;
// first subarray
for (int i = 0; i < k; i++) {
// only push the elements that may contribute to maximum
while (!d1.empty() && arr[d1.back()] <= arr[i]) {
d1.pop_back();
}
// only push the elements that may contribute to minimum
while (!d2.empty() && arr[d2.back()] >= arr[i]) {
d2.pop_back();
}
// add the current element's index
d1.push_back(i);
d2.push_back(i);
}
// sum of min and max for first subarray
sum += (arr[d2.front()] + arr[d1.front()]);
// traverse the remaining subarray
for (int i = k; i < n; i++) {
// remove the previous element (sliding window technique)
while (!d1.empty() && d1.front() <= (i -k)) {
d1.pop_front();
}
while (!d2.empty() && d2.front() <= (i - k)) {
d2.pop_front();
}
// only push the elements that may contribute to maximum
while (!d1.empty() && arr[d1.back()] <= arr[i]) {
d1.pop_back();
}
// only push the elements that may contribute to minimum
while (!d2.empty() && arr[d2.back()] >= arr[i]) {
d2.pop_back();
}
// add the current element's index
d1.push_back(i);
d2.push_back(i);
// sum of min and max for current subarray
sum += (arr[d1.front()] + arr[d2.front()]);
}
// return total sum
return sum;
}
int main() {
// Example 1
int arr1[] = {5, 9, 8, 3, -4, 2, 1, -5};
int k1 = 4;
cout<<sumOfMinMax(arr1, k1, sizeof(arr1) / sizeof(arr1[0]))<<endl;
// Example 2
int arr2[] = {1, -1, 2, -2, 3, -3};
int k2 = 2;
cout<<sumOfMinMax(arr2, k2, sizeof(arr2) / sizeof(arr2[0]))<<endl;
return 0;
}17 2
Complexity Analysis
Time Complexity = O(n)
Space Complexity = O(n)
where n is the total number of elements in the given array.
As we have used queues which represent the numbers in decreasing and increasing order, so they are storing the elements once. Thus the algorithm takes linear time, and thus the space required is also linear.