Implement Stack using Queues

Implement the following functions of stack data structure using standard operations of queue,

1. push(x) –> Push an element x to the stack
2. pop() –> Removes the element on top of stack
3. top() –> Return the element on top of stack
4. empty() –> Return whether the stack is empty

Examples

Input:
stack.push(1);
stack.push(2);
stack.top();  // returns 2
stack.pop();  // returns 2
stack.empty();  // returns false
Output:
2
2
false

Algorithm for Implement Stack using Queues

A stack can be implemented using 2 queues (say q1 and q2).

push(x)

Push x at the end of q1 and keep it as the top of the stack in top variable.
Pseudo Code

void push(int x) {
    q1.add(x);
    top = x;
}

Time Complexity= O(1)

top()

The top of the stack is always maintained in the top variable, so simply return the top.
Pseudo Code

int top() {
    return top;
}

Time Complexity = O(1)

empty()

The stack is empty if the queue q1 is empty.
Pseudo Code

boolean empty() {
    return q1.isEmpty();
}

Time Complexity = O(1)

pop()

The rear of queue q1 contains the top of the stack, let the size of q1 be n

1. Move (n – 1) elements of queue q1 to queue q2.
2. Also, maintain the top of stack as the current variable being transferred.
3. Now, q1 contains only 1 element that is top of the stack.
4. Remove and store this element in some variable (say ele).
5. Move all the elements from queue q2 to queue q1.
6. Return ele.

Time Complexity= O(n) 
where n is the number of elements in the queue.

Consider an example,
q1= 3 -> 5 -> 7 -> 1 -> 2
q2 = null

Pop out an element.

1. Transfer (n – 1) from q1 to q2
   q1 = 2 and q2=3 -> 5 -> 7 -> 1
2. Remove and store the element in q1.
   q1 = null and q2 =3 -> 5 -> 7 -> 1 and ele = 2
3. Move all the elements from q2 to q1.
   q1=3 -> 5 -> 7 -> 1 and q2 = null
4. Return ele.

See the image below for clarification.

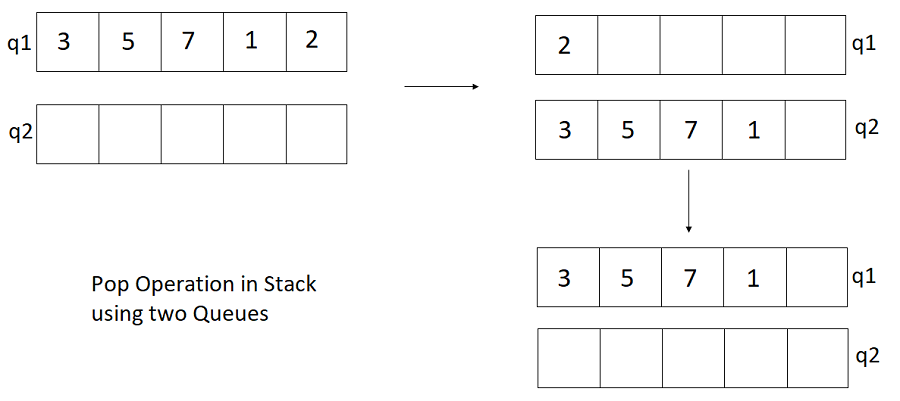
Pseudo Code

int pop() {
    int n = q1.size();
    for (int i = 0; i < n - 1; i++) {
        int curr = q1.remove();
        q2.add(curr);
        top = curr;
    }
    int ele = q1.remove();
    n = q2.size();
    for (int i = 0; i < n; i++) {
        q1.add(q2.remove());
    }
    return ele;
}

Time Complexity = O(n)

JAVA Code for Implement Stack using Queues

import java.util.Queue; 
import java.util.LinkedList;
public class StackUsingQueues {
    // Two queues to implement stack
    private static Queue<Integer> q1 = new LinkedList<>();
    private static Queue<Integer> q2 = new LinkedList<>();
    // Stores the top element of stack
    private static int top;

    private static void push(int x) {
        // Add element at rear of q1
        q1.add(x);
        // update top as current element
        top = x;
    }

    private static int top() {
        // Top stores the top of stack
        return top;
    }

    private static int pop() {
        int n = q1.size();
        // Shift (n - 1) elements from q1 to q2 and update top as curr
        // element transferred
        for (int i = 0; i < n - 1; i++) {
            int curr = q1.remove();
            q2.add(curr);
            top = curr;
        }
        // q1 contains only 1 element which is top of stack
        // store the element in ele and remove it from q1
        int ele = q1.remove();
        n = q2.size();
        // Again transfer back the elements from q2 to q1
        for (int i = 0; i < n; i++) {
            q1.add(q2.remove());
        }
        // return ele, this is the top of stack
        return ele;
    }
    
    private static boolean empty() {
        // If q1 is empty then stack is empty
        return q1.isEmpty();
    }
    
    public static void main(String[] args) {
        // Example
        push(1);
        push(2);
        System.out.println(top());
        System.out.println(pop());
        System.out.println(empty());
    }
}

C++ Code for Implement Stack using Queues

#include <bits/stdc++.h>
using namespace std;

// Two queues to implement stack
queue<int> q1;
queue<int> q2;
// Stores the top element of stack
int Top;

void push(int x) {
    // Add element at rear of q1
    q1.push(x);
    // update top as current element
    Top = x;
}

int top() {
    // Top stores the top of stack
    return Top;
}

bool empty() {
    // If q1 is empty then stack is empty
    return q1.empty();
}

int pop() {
    int n = q1.size();
    // Shift (n - 1) elements from q1 to q2 and update top as curr
    // element transferred
    for (int i = 0; i < n - 1; i++) {
        int curr = q1.front();
        q1.pop();
        q2.push(curr);
        Top = curr;
    }
    // q1 contains only 1 element which is top of stack
    // store the element in ele and remove it from q1
    int ele = q1.front();
    q1.pop();
    n = q2.size();
    // Again transfer back the elements from q2 to q1
    for (int i = 0; i < n; i++) {
        q1.push(q2.front());
        q2.pop();
    }
    // return ele, this is the top of stack
    return ele;
}

int main() {
    // Example
    push(1);
    push(2);
    cout<<top()<<endl;
    cout<<pop()<<endl;
    if (empty()) {
        cout<<"true"<<endl;
    } else {
        cout<<"false"<<endl;
    }
    return 0;
}

2
2
false

Reference1    reference2