Iterative Postorder Traversal Using Two Stacks

Problem Statement

The problem “Iterative Postorder Traversal Using Two Stacks” states that you are given a binary tree with n nodes. Write the program for it’s iterative postorder traversal using two stacks.

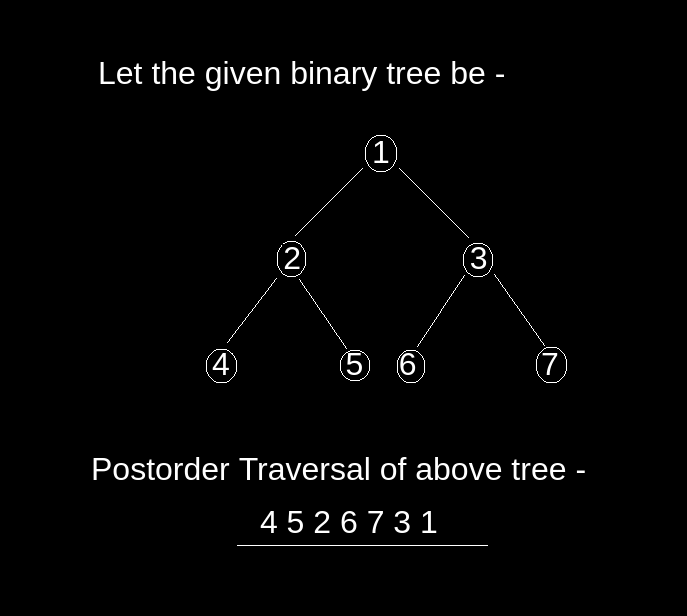
Example

Input

4 5 2 6 7 3 1

Input

4 2 3 1

Algorithm

1. Create a structure for the node consisting of an integer variable to hold the data and two-node type pointers left and right.
2. After that, create the function to create the new node which accepts an integer value as it’s parameter. Create a node inside it. Store the integer value passed as the parameter in its data variable and update the right and left pointer node as null. Return the newly created node.
3. Similarly, create the function for the iterative post order traversal which accepts the pointer to the root node of the binary tree. Check if the root node is equal to null, return.
4. Create two stack data structures of type Node* to help in the traversal.
5. Push / insert the root node in the stack 1. Create another new node.
6. While stack 1 is not empty i.e. size of the stack 1 is not equal to 0. Store the node at the top of the stack 1 in the new node and pop/remove it from the stack. Push/insert the removed node in the stack 2. Check if the left of the current node is present, push/insert it in the stack 1. Similarly, check if the right of the node is present, push it in the stack 1.
7. Traverse again while the stack 1 is not empty, store the node at the top of the stack 1 in the 2nd stack and pop it from the 1st stack.
8. At last print the 2nd node.

Code

C++ Program for Iterative Postorder Traversal Using Two Stacks

#include <bits/stdc++.h> 
using namespace std; 
  
struct Node{ 
    int data; 
    Node *left, *right; 
}; 
  
Node* newNode(int data){ 
    Node* node = new Node; 
    node->data = data; 
    node->left = node->right = NULL; 
    return node; 
} 

void postOrderIterative(Node* root){ 
    if(root == NULL){ 
        return; 
    }
  
    stack<Node *> s1, s2; 
  
    s1.push(root); 
    Node* node; 
  
    while(!s1.empty()){ 
        node = s1.top(); 
        s1.pop(); 
        s2.push(node); 
  
        if(node->left){ 
            s1.push(node->left);
        }
        if(node->right){ 
            s1.push(node->right);
        }
    } 
  
    while(!s2.empty()){ 
        node = s2.top(); 
        s2.pop(); 
        cout << node->data << " "; 
    } 
} 
  
int main(){ 
    Node* root = NULL; 
    root = newNode(1); 
    root->left = newNode(2); 
    root->right = newNode(3); 
    root->left->left = newNode(4); 
    root->left->right = newNode(5); 
    root->right->left = newNode(6); 
    root->right->right = newNode(7); 
  
    postOrderIterative(root); 
  
    return 0; 
}

4 5 2 6 7 3 1

Java Program for Iterative Postorder Traversal Using Two Stacks

import java.util.*; 

class IterativePostorder{ 
  
    static class node{ 
        int data; 
        node left, right; 
  
        public node(int data){ 
            this.data = data; 
        } 
    } 
  
    static Stack<node> s1, s2; 
  
    static void postOrderIterative(node root){ 
        s1 = new Stack<>(); 
        s2 = new Stack<>(); 
  
        if(root == null){ 
            return; 
        }
  
        s1.push(root); 
  
        while(!s1.isEmpty()){ 
            node temp = s1.pop(); 
            s2.push(temp); 
  
            if(temp.left != null){ 
                s1.push(temp.left);
            }
            
            if(temp.right != null){ 
                s1.push(temp.right);
            }
        } 
  
        while(!s2.isEmpty()){ 
            node temp = s2.pop(); 
            System.out.print(temp.data + " "); 
        } 
    } 
  
    public static void main(String[] args){ 
        
        node root = null; 
        root = new node(1); 
        root.left = new node(2); 
        root.right = new node(3); 
        root.left.left = new node(4); 
        root.left.right = new node(5); 
        root.right.left = new node(6); 
        root.right.right = new node(7); 
  
        postOrderIterative(root); 
    } 
}

4 5 2 6 7 3 1

Complexity Analysis

Time Complexity

O(n) where n is the number of nodes inserted.

Space Complexity

O(n) because we used space for n nodes.