Check whether a given Binary Tree is Complete or not

Problem Statement

The problem “Check whether a given Binary Tree is Complete or not” states that you are given the root of a binary tree, check whether the tree is complete or not. A complete Binary Tree has all its levels filled except for the last level and the nodes in the last level are as left as possible.

Examples

Input

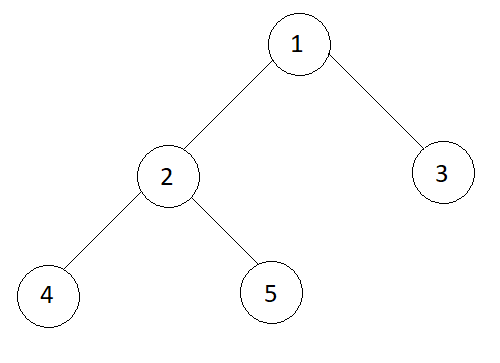
true

Input

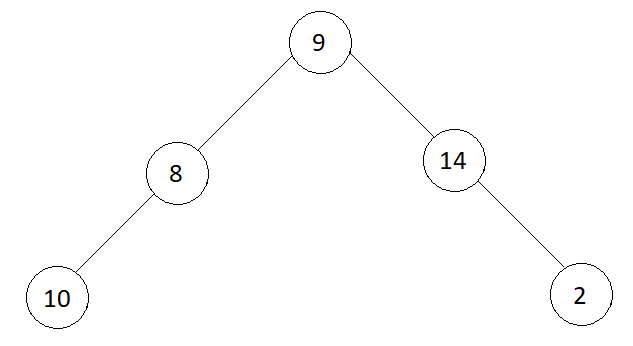
false

Approach

A complete Binary tree is a binary tree in which all the levels are filled except for the last level and the last level nodes are as left as possible.

To check if a binary tree is complete or not, we can use the level order traversal of the tree.

1. Define a complete node as the node that has both left and right child as not null.
2. For a complete tree, if we see a non complete node during level order traversal, then all the nodes after this node has to be leaf nodes, else the tree is not complete.
3. Also if there is a node with right child as not null and left child as null, the tree is not complete.

Algorithm

1. If the root is null, return true.
2. Create a queue and push the root node to it. Initialize a boolean variable foundNonComplete as false.
3. While the queue is not empty repeat step 4.
4. Remove a node from the queue, let it be current node. If left child of current node is not null, check if foundNonComplete is true, if yes return false, else push the left child to the queue, if the left child is null, mark foundNonComplete as true. Similarly, if the right child is not null, check if foundNonComplete is true, if yes return false, else push the right child to queue, if right child is null mark foundNonComplete as true.
5. If we reach step 5, return true.

Code

Java Code to Check whether a given Binary Tree is Complete or not

import java.util.LinkedList;
import java.util.Queue;
class CheckWhetherAGivenBinaryTreeIsCompleteOrNot {
    // class representing the node of a binary tree
    static class Node {
        int data;
        Node left, right;

        public Node(int data) {
            this.data = data;
        }
    }

    private static boolean isComplete(Node root) {
        // if root is null, return true
        if (root == null) {
            return true;
        }

        // create a queue to do level order traversal
        Queue<Node> queue = new LinkedList<>();
        // add the root node to queue
        queue.add(root);
        // initialize foundNonComplete as false
        boolean foundNonComplete = false;

        while (!queue.isEmpty()) {
            // remove a node from queue
            Node curr = queue.poll();
            if (curr.left != null) {
                // if a non complete node was found, return false
                if (foundNonComplete) {
                    return false;
                }
                // add the left child to queue
                queue.add(curr.left);
            } else {
                // if left child is null, this is a non complete node
                foundNonComplete = true;
            }

            if (curr.right != null) {
                // if a non complete node was found, return false
                if (foundNonComplete) {
                    return false;
                }
                // add the right child to queue
                queue.add(curr.right);
            } else {
                // if right child is null, this is a non complete node
                foundNonComplete = true;
            }
        }

        // reaching here means tree is complete
        return true;
    }

    public static void main(String[] args) {
        // Example 1
        Node root1 = new Node(1);
        root1.left = new Node(2);
        root1.right = new Node(3);
        root1.left.left = new Node(4);
        root1.left.right = new Node(5);
        System.out.println(isComplete(root1));

        // Example 2
        Node root2 = new Node(9);
        root2.left = new Node(8);
        root2.right = new Node(14);
        root2.left.left = new Node(10);
        root2.right.right = new Node(2);
        System.out.println(isComplete(root2));
    }
}

true
false

C++ Code to Check whether a given Binary Tree is Complete or not

#include <bits/stdc++.h> 
using namespace std; 

// class representing the node of a binary tree
class Node {
    public:
    int data;
    Node *left;
    Node *right;
    
    Node(int d) {
        data = d;
        left = right = NULL;
    }
};

bool isComplete(Node *root) {
    // if root is null, return true
    if (root == NULL) {
        return true;
    }
    
    // create a queue to do level order traversal
    queue<Node*> q;
    // add the root node to queue
    q.push(root);
    // initialize foundNonComplete as false
    bool foundNonComplete = false;
    
    while (!q.empty()) {
        // remove a node from queue
        Node *curr = q.front();
        q.pop();
        if (curr->left != NULL) {
            // if a non complete node was found, return false
            if (foundNonComplete)
                return false;
            // add the left child to queue
            q.push(curr->left);
        } else {
            // if left child is null, this is a non complete node
            foundNonComplete = true;
        }
        
        if (curr->right != NULL) {
            // if a non complete node was found, return false
            if (foundNonComplete) 
                return false;
            q.push(curr->right);
        }
    }
    
    // reaching here means tree is complete
    return true;
}

int main() {
    // Example 1
    Node *root1 = new Node(1);
    root1->left = new Node(2);
    root1->right = new Node(3);
    root1->left->left = new Node(4);
    root1->left->right = new Node(5);
    if (isComplete(root1)) {
        cout<<"true"<<endl;
    } else {
        cout<<"false"<<endl;
    }

    // Example 2
    Node *root2 = new Node(9);
    root2->left = new Node(8);
    root2->right = new Node(14);
    root2->left->left = new Node(10);
    root2->right->right = new Node(2);
    if (isComplete(root2)) {
        cout<<"true"<<endl;
    } else {
        cout<<"false"<<endl;
    }
    
    return 0;
}

true
false

Complexity Analysis

Time Complexity

O(N), as we have only done level order traversal of the binary tree. The level order traversal traverses through the tree nodes. Thus the algorithm runs in linear time complexity.

Space Complexity

O(N), the level order traversal requires the use of queue which makes the algorithm to have linear space complexity.