Given a tree (an acyclic fully connected graph where constituent nodes are connected by bidirectional edges) and a source node. find the level of each node in a tree form source node. It is given that level of a node v with respect to the source is the distance between source and v.
Table of Contents
Example
Consider the graph given below with 0 as the source node.
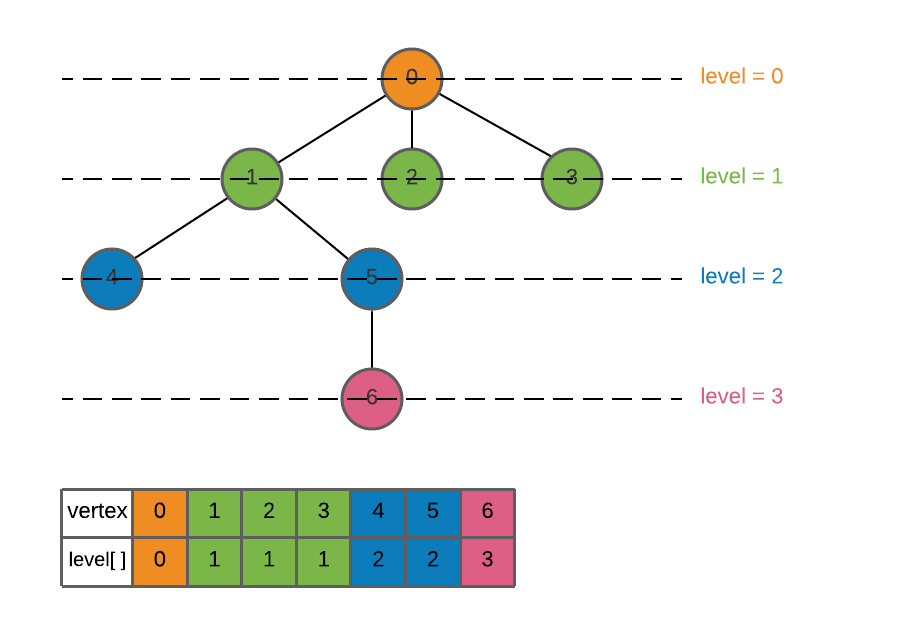
Types of solution
- Depth first search
- Breadth first search
Depth first search
Approach for Level of Each node in a Tree from the source node
We perform depth first search (DFS) from source node to every other node in the graph. A level[ ] array stores level of each node in the graph with respect to source node. The level of source node with respect to itself is 0 (distance of a node from itself is 0), for a current node during DFS traversal consider top is the unvisited neighbor of current.On visiting top ,we simply mark it as visited and make following assignment level[top] = level[current] + 1 . After this, we simply make DFS traversal (recursively) with the top as a source node.
Algorithm
- Define number of vertices and decide the source node.
- construct the given graph.
- create level[ ] and vis[ ] arrays.level[ ] stores level of each node w.r.t. source node and vis[ ] stores whether a particular vertex has been visited previously or not.
- Perform DFS traversal from the source node.
- for a given current node during DFS traversal consider top is the unvisited neighbor of current. On visiting top ,we simply mark it as visited and make following assignment level[top] = level[current] + 1.
- Now recursively perform DFS traversal from top vertex to its neighbors.
- The DFS traversal is to be done until all the vertices have been visited once. once you visit/process a node in the graph, mark it as visited.
- After traversal is over, simply print level of each node stored in level[ ] array.



Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function to link nodes u and v */
void addEdge(vector <int> graph[],int u,int v)
{
graph[u].push_back(v);
graph[v].push_back(u);
}
/* function to perform depth first search and
evaluate level of each node w.r.t. to source node */
void DFS(int source,vector <int> graph[],vector <int> &level,vector <bool> &vis)
{
vis[source] = true;
for(auto i:graph[source])
{
if(!vis[i])
{
vis[i] = true;
level[i] = level[source]+1;
DFS(i,graph,level,vis);
}
}
}
int main()
{
/* define number of vertices and
source vertex in the graph */
int vertex = 7;
int source = 0;
/* construct the graph and link the nodes through edges */
vector <int> graph[vertex];
addEdge(graph,0,1);
addEdge(graph,0,2);
addEdge(graph,0,3);
addEdge(graph,1,4);
addEdge(graph,1,5);
addEdge(graph,5,6);
/* level[i] stores level of i-th node with respect to source node
level of a node is distance of that node from the source node */
vector <int> level(vertex,0);
/* vis[] is used to check whether a node has been visited during DFS */
vector <bool> vis(vertex,0);
/* perform DFS of given graph from source node */
DFS(source,graph,level,vis);
/* output level of each node in the graph */
cout<<"The levels of each node with respect to "<<source<<"-node is given below:"<<endl;
cout<<"Node"<<" "<<"Level"<<endl;
for(int i=0;i<vertex;i++)
cout<<i<<"\t"<<level[i]<<endl;
return 0;
}The levels of each node with respect to 0-node is given below: Node Level 0 0 1 1 2 1 3 1 4 2 5 2 6 3
Java Program
import java.util.*;
import java.io.*;
class TutorialCup
{
/* function to link nodes u and v */
static void addEdge(ArrayList<ArrayList<Integer>> graph,int u,int v)
{
graph.get(u).add(v);
graph.get(v).add(u);
}
/* function to perform depth first search and
evaluate level of each node w.r.t. to source node */
static void DFS(int source,ArrayList<ArrayList<Integer>> graph,int [] level,boolean [] vis)
{
vis[source] = true;
Iterator it = graph.get(source).iterator();
while(it.hasNext())
{
int i = (Integer)it.next();
if(!vis[i])
{
vis[i] = true;
level[i] = level[source] + 1;
DFS(i,graph,level,vis);
}
}
}
public static void main (String[] args)
{
/* define number of vertices and
source vertex in the graph */
int vertex = 7;
int source = 0;
/* construct the graph and link the nodes through edges */
ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
for(int i=0;i<vertex;i++)
graph.add(new ArrayList<Integer>());
addEdge(graph,0,1);
addEdge(graph,0,2);
addEdge(graph,0,3);
addEdge(graph,1,4);
addEdge(graph,1,5);
addEdge(graph,5,6);
/* level[i] stores level of i-th node with respect to source node
level of a node is distance of that node from the source node */
int [] level = new int[vertex];
/* vis[] is used to check whether a node has been visited during DFS */
boolean [] vis = new boolean[vertex];
/* perform DFS of given graph from source node */
DFS(source,graph,level,vis);
/* output level of each node in the graph */
System.out.println("The levels of each node with respect to "+source+"-node is given below:");
System.out.println("Node"+" "+"Level");
for(int i=0;i<vertex;i++)
System.out.println(i+"\t"+level[i]);
}
}The levels of each node with respect to 0-node is given below: Node Level 0 0 1 1 2 1 3 1 4 2 5 2 6 3
Complexity Analysis for Level of Each node in a Tree from the source node
- Time complexity: T(n) = O(V+E).
- Space Complexity: A(n) = O(1), recursive approach.
V = number of vertices.
E = number of edges.
Breadth first search
Approach for Level of Each node in a Tree from the source node
We perform the breadth first search (BFS) from the source node to every other node in the graph. The queue data structure is used to perform BFS traversal. A level[ ] array stores the level of each node in the graph with respect to the source node. The level of source node with respect to itself is 0 (the distance of a node from itself is 0), for a current node during BFS traversal consider top is the unvisited neighbor of current and present at front of the queue. On visiting top (after popping top from the queue), we simply mark it as visited and make following assignment level[top] = level[current] + 1. After this, we simply add all the unvisited neighbors of top to the queue.
The objective of the queue data structure is to store all the unvisited neighboring vertices of the current element so that they can later be visited in an iterative manner.
Algorithm
- Define the number of vertices and decide the source node.
- Construct the given graph.
- Create level[ ] and vis[ ] arrays.level[ ] stores level of each node w.r.t. source node and vis[ ] stores whether a particular vertex has been visited previously or not.
- Perform BFS iterative traversal from the source node.
- Begin traversal and pop a node top from the queue.
- Visit all its unvisited neighbor n1,n2 …. and mark them as visited.
- Make the following assignment for each unvisited neighbor: level[n1] = level[top] + 1 and insert them into the queue.
- Iteratively perform BFS from each of the nodes present in the queue popping them one by one.
- The BFS traversal is to be done until all the vertices have been visited once. once you visit/process a node in the graph, mark it as visited.
- After traversal is over, simply print the level of each node stored in level[ ] array.


Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function to link nodes u and v */
void addEdge(vector <int> graph[],int u,int v)
{
graph[u].push_back(v);
graph[v].push_back(u);
}
/* function to perform breadth first search and
evaluate level of each node w.r.t. to source node */
void BFS(int source,vector <int> graph[],vector <int> &level,vector <bool> &vis)
{
queue <int> q;
q.push(source);
while(!q.empty())
{
int top = q.front();
vis[top] = true;
q.pop();
for(auto i : graph[top])
{
if(!vis[i])
{
level[i] = level[top] + 1;
q.push(i);
}
}
}
}
int main()
{
/* define number of vertices and
source vertex in the graph */
int vertex = 7;
int source = 0;
/* construct the graph and link the nodes through edges */
vector <int> graph[vertex];
addEdge(graph,0,1);
addEdge(graph,0,2);
addEdge(graph,0,3);
addEdge(graph,1,4);
addEdge(graph,1,5);
addEdge(graph,5,6);
/* level[i] stores level of i-th node with respect to source node
level of a node is distance of that node from the source node */
vector <int> level(vertex,0);
/* vis[] is used to check whether a node has been visited during DFS */
vector <bool> vis(vertex,0);
/* perform DFS of given graph from source node */
BFS(source,graph,level,vis);
/* output level of each node in the graph */
cout<<"The levels of each node with respect to "<<source<<"-node is given below:"<<endl;
cout<<"Node"<<" "<<"Level"<<endl;
for(int i=0;i<vertex;i++)
cout<<i<<"\t"<<level[i]<<endl;
return 0;
}The levels of each node with respect to 0-node is given below: Node Level 0 0 1 1 2 1 3 1 4 2 5 2 6 3
Java Program
import java.util.*;
import java.io.*;
class TutorialCup
{
/* function to link nodes u and v */
static void addEdge(ArrayList<ArrayList<Integer>> graph,int u,int v)
{
graph.get(u).add(v);
graph.get(v).add(u);
}
/* function to perform breadth first search and
evaluate level of each node w.r.t. to source node */
static void BFS(int source,ArrayList<ArrayList<Integer>> graph,int [] level,boolean [] vis)
{
Queue <Integer> q = new LinkedList<>();
q.add(source);
while(!q.isEmpty())
{
int top = q.poll();
vis[top] = true;
Iterator it = graph.get(top).iterator();
while(it.hasNext())
{
int i = (Integer)it.next();
if(!vis[i])
{
level[i] = level[top] + 1;
q.add(i);
}
}
}
}
public static void main (String[] args)
{
/* define number of vertices and
source vertex in the graph */
int vertex = 7;
int source = 0;
/* construct the graph and link the nodes through edges */
ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
for(int i=0;i<vertex;i++)
graph.add(new ArrayList<Integer>());
addEdge(graph,0,1);
addEdge(graph,0,2);
addEdge(graph,0,3);
addEdge(graph,1,4);
addEdge(graph,1,5);
addEdge(graph,5,6);
/* level[i] stores level of i-th node with respect to source node
level of a node is distance of that node from the source node */
int [] level = new int[vertex];
/* vis[] is used to check whether a node has been visited during DFS */
boolean [] vis = new boolean[vertex];
/* perform DFS of given graph from source node */
BFS(source,graph,level,vis);
/* output level of each node in the graph */
System.out.println("The levels of each node with respect to "+source+"-node is given below:");
System.out.println("Node"+" "+"Level");
for(int i=0;i<vertex;i++)
System.out.println(i+"\t"+level[i]);
}
}The levels of each node with respect to 0-node is given below: Node Level 0 0 1 1 2 1 3 1 4 2 5 2 6 3
Complexity Analysis for Level of Each node in a Tree from the source node
- Time complexity: T(n) = O(V+E).
- Space Complexity: A(n) = O(V), queue data structure used.
V = number of vertices.
E = number of edges.