Maximum Depth Of Binary Tree

Problem Statement

“Maximum depth of binary tree” problem states that you are given a binary tree data structure. Print the maximum depth of the given binary tree.

Example

Input

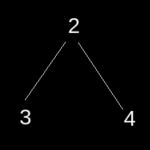
2

Explanation: Maximum depth for the given tree is 2. Because there is only a single element below the root (i.e. at a greater depth than root level = 1) in both left and right subtree.

Input

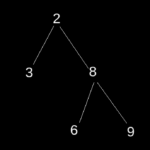
3

Explanation: There are two elements at level =3, in the right subtree. Thus maximum depth = 3.

Algorithm for maximum depth of binary tree

1. Initialize a binary tree data structure.
2. Create a class node with a variable of integer type and the two-node type pointers left and right as it's private members.
3. Create a function newNode to create a new node of the binary tree which accepts a variable of integer type consisting of data as it's a parameter.
4. After that, initialize a new node inside it. Store the integer variable given as a parameter in the data of the node of the binary tree and update the value of it's left and the right pointer is null.
5. Return the newly created node.
6. Similarly, create a function to find the maximum depth of the binary tree which accepts a node pointer as it's a parameter.
7. Check if the node is equal to null, return 0.
8. Else create a variable left of integer type representing the depth of the left subtree. Make a recursive call to the function itself with the left of the node as it's a parameter and store the result returned in the variable left.
9. Similarly, create a variable right of integer type representing the depth of the right subtree. Make a recursive call to the function itself with the right of the node as it's a parameter and store the result returned in the variable right.
10. After that, check if the depth of the left subtree is greater than the depth of the right subtree return the depth of the left subtree + 1.
11. Else return the variable right i.e. the depth of the right subtree + 1.

In a binary tree data structure, we have left and right nodes, which then itself have left and right bodes. Thus, making a tree-like data structure. In a binary tree, nodes are connected to make subtrees. So, we define some terminology for the binary tree data structure. And one of them is maximum depth, which is defined as the maximum height of the tree the distance from the root to leaf. A leaf is nothing but a node that does not have either the left or right node.

For finding the maximum depth we calculate the depth of left and right subtree. The depth of the current tree is equal to the maximum of left and right subtree +1. Thus we use a recursive approach to find the depth of left and right subtree. Since we are using recursion, we must have some base cases. Here the base case is if we are at a node which is a leaf. A leaf node has length = 1.

Code

C++ Program to find maximum depth of binary tree

#include <bits/stdc++.h> 
using namespace std; 
  
class node{  
    public: 
        int data;  
        node* left;  
        node* right;  
};  
  
int maxDepth(node* node){  
    if(node == NULL)  
        return 0;  
    else{  
        int left = maxDepth(node->left);  
        int right = maxDepth(node->right);  
      
        if(left > right)  
            return(left + 1);  
        else return(right + 1);  
    }  
}  
  
node* newNode(int data){  
    node* Node = new node(); 
    Node->data = data;  
    Node->left = NULL;  
    Node->right = NULL;  
      
    return(Node);  
}  
      
int main(){  
    node *root = newNode(2);  
  
    root->left = newNode(3);  
    root->right = newNode(8);  
    root->left->left = newNode(6);  
    root->left->right = newNode(9);  
      
    cout<<maxDepth(root);  
    return 0;  
}

3

Java Program to find maximum depth of binary tree

class Node{ 
    int data; 
    Node left, right; 
   
    Node(int item){ 
        data = item; 
        left = right = null; 
    } 
} 
   
class BinaryTree{ 
     Node root; 
   
    int maxDepth(Node node){ 
        if(node == null) 
            return 0; 
        else{ 
            int left = maxDepth(node.left); 
            int right = maxDepth(node.right); 
   
            if(left > right) 
                return (left + 1); 
             else 
                return (right + 1); 
        } 
    } 
       
    public static void main(String[] args){ 
        BinaryTree tree = new BinaryTree(); 
   
        tree.root = new Node(2); 
        tree.root.left = new Node(3); 
        tree.root.right = new Node(8); 
        tree.root.left.left = new Node(6); 
        tree.root.left.right = new Node(9); 
   
        System.out.println(tree.maxDepth(tree.root)); 
    } 
}

3

Complexity Analysis

Time Complexity

O(N) where n is the number of data nodes inserted in the given binary tree.

Space Complexity

O(1) because we used constant extra space.

References