Consider a binary search tree, two nodes of the tree have been swapped, design an algorithm to recover the binary search Tree.
Example
Consider the binary search tree given below whose two nodes have been swapped as input.

Incorrect nodes on the BST are detected(highlighted) and then swapped to obtain the correct BST.
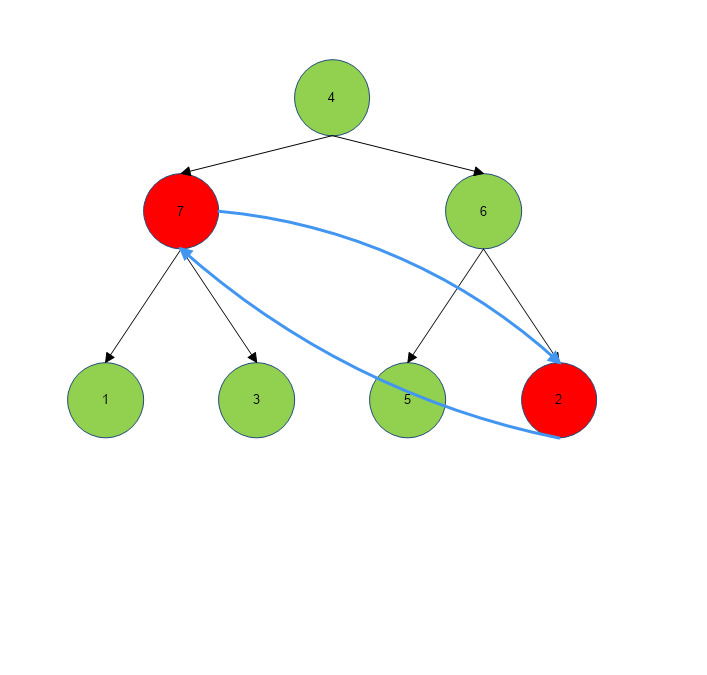
Below is the corrected output BST obtained after swapping the incorrect nodes.
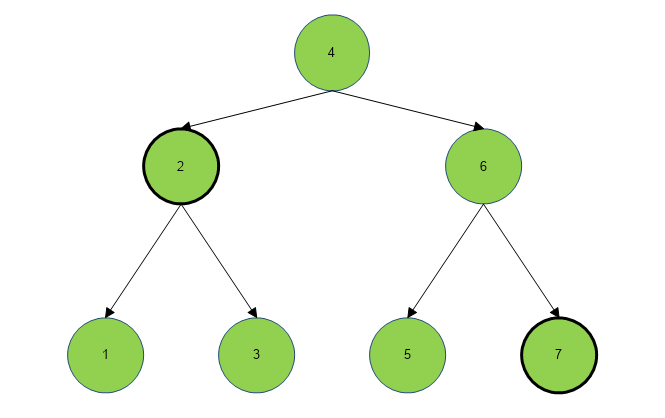
Table of Contents
Types of Solution for Recover Binary Search Tree
- Naive
- Recursive
- Iterative
- Morris Traversal
Naive
Approach for Recover Binary Search Tree
Use vector to store all the elements of the tree using inorder traversal, sort this vector. Again, Perform inorder traversal of the tree and assign values from sorted vector to tree nodes one by one.
Algorithm
- Perform inorder traversal of the tree and store the traversal in a dynamic array.
- Sort the dynamic array using insertion sort(for minimum complexity).
- Perform the inorder traversal again and change the node values to values from the sorted array.
- Return the root node of the corrected binary search tree.
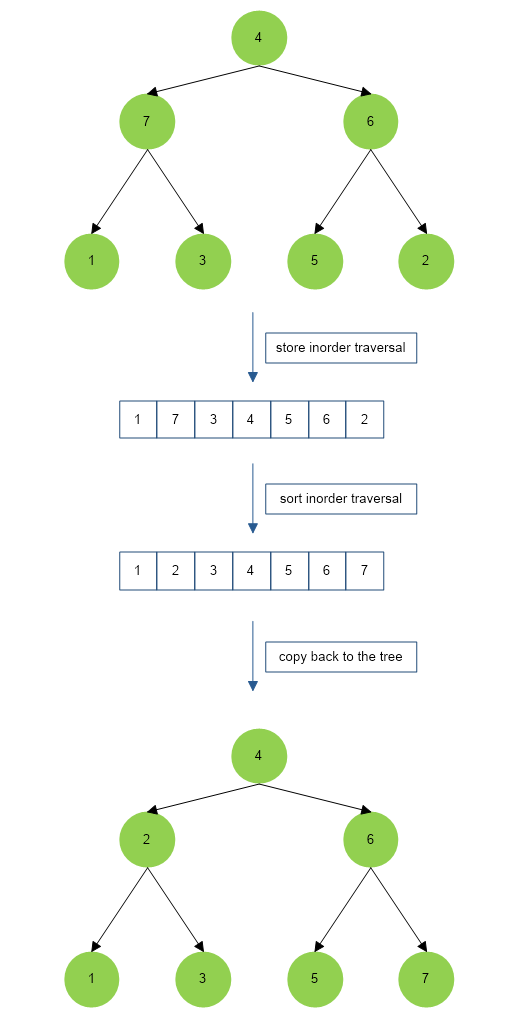
Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
// function that performs inorder traversal based on the mode
/*
Their are 3 modes :
1. traversal ('t') : simply perform traversal
2. storage ('s') : store data of tree into a vector
3. modify ('m'): store data of vector into a tree
*/
void inorder(Node *root,vector <int> &arr,char mode)
{
if(!root)
return;
inorder(root->left,arr,mode);
if(mode == 't')
cout<<root->data<<" ";
else if(mode == 's')
arr.push_back(root->data);
else if(mode == 'm')
{
int n = arr.size();
root->data = arr[n-1];
arr.pop_back();
}
inorder(root->right,arr,mode);
}
// function that corrects the BST and returns it's root
Node* fixBST(Node *root)
{
// array to store inorder traversal
vector <int> arr;
// store the inorder traversal into arr
inorder(root,arr,'s');
// apply insertion sort to arr
// insertion sort is used to minimize time complexity to o(n)
int i,j,key;
for (i = 1; i < arr.size(); i++)
{
key = arr[i];
j = i - 1;
while (j >= 0 && arr[j] < key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
// perform inorder on tree and modify the the node value of tree
inorder(root,arr,'m');
return root;
}
int main()
{
/* create the incorrect BST*/
Node *root = new Node(4);
root->left = new Node(7);
root->right = new Node(6);
root->left->left = new Node(1);
root->left->right = new Node(3);
root->right->left = new Node(5);
root->right->right = new Node(2);
vector <int> arr;
cout<<"Inorder traversal before : ";
inorder(root,arr,'t');
root = fixBST(root);
cout<<endl;
cout<<"Inorder traversal after : ";
inorder(root,arr,'t');
return 0;
}Inorder traversal before : 1 7 3 4 5 6 2 Inorder traversal after : 1 2 3 4 5 6 7
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
// function that performs inorder traversal based on the mode
/*
Their are 3 modes :
1. traversal ('t') : simply perform traversal
2. storage ('s') : store data of tree into a vector
3. modify ('m'): store data of vector into a tree
*/
static void inorder(Node root,ArrayList <Integer> arr,char mode)
{
if(root == null)
return;
inorder(root.left,arr,mode);
if(mode == 't')
System.out.print(root.data+" ");
else if(mode == 's')
arr.add(root.data);
else if(mode == 'm')
{
int n = arr.size();
root.data = arr.get(n-1);
arr.remove(n-1);
}
inorder(root.right,arr,mode);
}
// function that corrects the BST and returns it's root
static Node fixBST(Node root)
{
// array to store inorder traversal
ArrayList <Integer> arr = new ArrayList<>();
// store the inorder traversal into arr
inorder(root,arr,'s');
// apply insertion sort to arr
// insertion sort is used to minimize time complexity to o(n)
int i,j,key;
for (i = 1; i < arr.size(); i++)
{
key = arr.get(i);
j = i - 1;
while (j >= 0 && arr.get(j) < key)
{
arr.set(j+1,arr.get(j));
j = j - 1;
}
arr.set(j+1,key);
}
// perform inorder on tree and modify the the node value of tree
inorder(root,arr,'m');
return root;
}
public static void main (String[] args)
{
/* create the incorrect BST*/
Node root = new Node(4);
root.left = new Node(7);
root.right = new Node(6);
root.left.left = new Node(1);
root.left.right = new Node(3);
root.right.left = new Node(5);
root.right.right = new Node(2);
ArrayList <Integer> arr = new ArrayList<>();
System.out.print("Inorder traversal before : ");
inorder(root,arr,'t');
root = fixBST(root);
System.out.println();
System.out.print("Inorder traversal after : ");
inorder(root,arr,'t');
}
}Inorder traversal before : 1 7 3 4 5 6 2 Inorder traversal after : 1 2 3 4 5 6 7
Complexity Analysis for Recover Binary Search Tree
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(n)
Recursive
Approach for Recover Binary Search Tree
- Consider the Tree given in the above example. The nodes of the BST can be swapped in two ways.
- 1st way: 2 non-adjacent tree nodes are swapped (i.e. these nodes have at least one node between them. for ex: inorder traversal of the tree where non-adjacent nodes are swapped is: 1 7 3 4 5 6 2. As we observe 2 and 7 are swapped from their respective positions.
- We perform the inorder traversal and use first and second variables to store the two incorrectly placed nodes. we use prev to store the previous node visited before the current (root) node during inorder traversal.
- During inorder traversal, we find a node that violates the BST order. i.e. prev->data > root->data(where root is the current node being visited), we store prev into first and root into second.
- During further traversal, if we find another node that violates the BST criteria (as mentioned above), but this time the first node has been already assigned a value. so we assign the current node to second.
- After the traversal is over, we swap the data stored in the first and second nodes.
- 2nd way: 2 adjacent nodes are swapped (i.e. the nodes are parent-child pair).for ex: inorder traversal of the tree where adjacent nodes are swapped is: 1 2 4 3 5 6 7. As we observe 3 and 4 are swapped from their respective positions.
- We perform the inorder traversal and use first and second variables to store the two incorrectly placed nodes. we use prev to store the previous node visited before the current (root) node during inorder traversal.
- During inorder traversal, we find a node that violates the BST order. i.e. prev->data > root->data(where root is the current node being visited), we store prev into first and root into second.
- After the traversal is over, we swap the data stored in the first and second nodes.
Algorithm
- Define prev(stores previous nodes in traversal), first(stores first node out of order), second(stores second node out of order) variables to store various tree node addresses.
- Perform simple inorder traversal.
- If during inorder traversal, we find a node that violates the BST order. i.e. prev->data > root->data.we store prev into first and root into second.
- During further traversal, if we find another node that violates the BST criteria,i.e. prev->data > root->data. but this time the first node had been already assigned a value. so we assign the current node to second.
- After execution of inorder traversal. swap the data of first and second nodes.The tree is fixed.

Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
/* function that performs inorder traversal
and checks for the incorrectly set nodes*/
void inorderFix(Node *root,Node* &prev,Node* &first,Node* &second)
{
if(root == NULL)
return;
inorderFix(root->left,prev,first,second);
if(prev != NULL && prev->data > root->data)
{
// first misordering found
if(first == NULL)
{
first = prev;
second = root;
}
// second misordering found (if exists)
else
second = root;
}
prev = root;
inorderFix(root->right,prev,first,second);
}
// function that corrects the BST and returns it's root
Node* fixBST(Node *root)
{
Node *prev,*first,*second;
prev = first = second = NULL;
inorderFix(root,prev,first,second);
swap(first->data,second->data);
return root;
}
// function to simply perform inorder traversal of the tree
void inorder(Node *root)
{
if(root == NULL)
return;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
int main()
{
/* create the incorrect BST*/
Node *root = new Node(4);
root->left = new Node(7);
root->right = new Node(6);
root->left->left = new Node(1);
root->left->right = new Node(3);
root->right->left = new Node(5);
root->right->right = new Node(2);
cout<<"Inorder traversal before : ";
inorder(root);
root = fixBST(root);
cout<<endl;
cout<<"Inorder traversal after : ";
inorder(root);
return 0;
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
/* function that performs inorder traversal
and checks for the incorrectly set nodes*/
static void inorderFix(Node root,ArrayList <Node> nodes)
{
if(root == null)
return;
inorderFix(root.left,nodes);
if(nodes.get(0) != null && nodes.get(0).data > root.data)
{
// first misordering found
if(nodes.get(1) == null)
{
// first is set to previous
nodes.set(1,nodes.get(0));
// second is set to current node
nodes.set(2,root);
}
// second misordering found (if exists)
else
nodes.set(2,root);
}
// 1st element of ArrayList stores previous nodes
nodes.set(0,root);
inorderFix(root.right,nodes);
}
// function that corrects the BST and returns it's root
/*
here,
prev -> nodes.get(0)
first -> nodes.get(1)
second -> nodes.get(2)
*/
static Node fixBST(Node root)
{
// we use ArrayList to store previous(nodes[0]),first(nodes[1]) and second(nodes[2])
// initially all nodes are set to null
ArrayList <Node> nodes = new ArrayList<>(Arrays.asList(null,null,null));
inorderFix(root,nodes);
// swap the values of the nodes
int temp = nodes.get(1).data;
nodes.get(1).data = nodes.get(2).data;
nodes.get(2).data = temp;
return root;
}
// function to simply perform inorder traversal of the tree
static void inorder(Node root)
{
if(root == null)
return;
inorder(root.left);
System.out.print(root.data+" ");
inorder(root.right);
}
public static void main (String[] args)
{
/* create the incorrect BST*/
Node root = new Node(4);
root.left = new Node(7);
root.right = new Node(6);
root.left.left = new Node(1);
root.left.right = new Node(3);
root.right.left = new Node(5);
root.right.right = new Node(2);
System.out.print("Inorder Traversal before : ");
inorder(root);
root = fixBST(root);
System.out.println();
System.out.print("Inorder Traversal after : ");
inorder(root);
}
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Complexity Analysis for Recover Binary Search Tree
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(n), recursion stack space used.
Iterative
Approach for Recover Binary Search Tree
The idea is to convert the above recursive code into an iterative code.
Algorithm
- Define prev(stores previous nodes in traversal), first(stores first node out of order), second(stores second node out of order) variables to store various tree node addresses.
- Perform simple inorder traversal.
- If during inorder traversal, we find a node that violates the BST order. i.e. prev->data > root->data.we store prev into first and root into second.
- During further traversal, if we find another node that violates the BST criteria,i.e. prev->data > root->data. but this time the first node had been already assigned a value. so we assign the current node to second.
- After execution of inorder traversal. swap the data of the first and second nodes. The tree is fixed.

Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
// function that corrects the BST by performing iterative inorder
// and returns it's root
Node* fixBST(Node *root)
{
Node *prev,*first,*second;
prev = first = second = NULL;
Node* curr = root;
stack <Node*> st;
while(!st.empty() || root != NULL)
{
if(root != NULL)
{
// visit current node's (root) left subtree
st.push(root);
root = root->left;
}
else
{
// done left subtree of current node
root = st.top();
st.pop();
// compare root.val with root.val if we have one
if(prev != NULL && root->data < prev->data)
{
// incorrect smaller node is always found as prev node
if(first == NULL)
first = prev;
// incorrect larger node is always found as current root node
second = root;
}
// visit root's right subtree
prev = root;
root = root->right;
}
}
// fix the BST by swapping values
int temp = first->data;
first->data = second->data;
second->data = temp;
// return address of the original root node
return curr;
}
// function to simply perform inorder traversal of the tree
void inorder(Node *root)
{
if(root == NULL)
return;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
int main()
{
/* create the incorrect BST*/
Node *root = new Node(4);
root->left = new Node(7);
root->right = new Node(6);
root->left->left = new Node(1);
root->left->right = new Node(3);
root->right->left = new Node(5);
root->right->right = new Node(2);
cout<<"Inorder traversal before : ";
inorder(root);
root = fixBST(root);
cout<<endl;
cout<<"Inorder traversal after : ";
inorder(root);
return 0;
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
// function that corrects the BST and returns it's root
static Node fixBST(Node root)
{
Node prev,first,second;
prev = first = second = null;
Node curr = root;
Stack<Node> st = new Stack<Node>();
while(!st.isEmpty() || root != null)
{
if(root != null)
{
// visit current node's (root) left subtree
st.push(root);
root = root.left;
}
else
{
// done left subtree of current node
root = st.pop();
// compare root.val with root.val if we have one
if(prev != null && root.data <= prev.data)
{
// incorrect smaller node is always found as prev node
if(first == null)
first = prev;
// incorrect larger node is always found as current root node
second = root;
}
// visit root's right subtree
prev = root;
root = root.right;
}
}
// fix the BST by swapping values
int temp = first.data;
first.data = second.data;
second.data = temp;
// return address of the original root node
return curr;
}
// function to simply perform inorder traversal of the tree
static void inorder(Node root)
{
if(root == null)
return;
inorder(root.left);
System.out.print(root.data+" ");
inorder(root.right);
}
public static void main (String[] args)
{
/* create the incorrect BST*/
Node root = new Node(4);
root.left = new Node(7);
root.right = new Node(6);
root.left.left = new Node(1);
root.left.right = new Node(3);
root.right.left = new Node(5);
root.right.right = new Node(2);
System.out.print("Inorder Traversal before : ");
inorder(root);
root = fixBST(root);
System.out.println();
System.out.print("Inorder Traversal after : ");
inorder(root);
}
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Complexity Analysis for Recover Binary Search Tree
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(n)
Morris Traversal
Approach for Recover Binary Search Tree
The idea is to basically perform inorder Morris traversal of the tree. Morris traversal ensures that traversal takes place in linear time and constant space (not even recursion stack space).
Morris traversal is similar to recursive/iterative traversal, but we need to modify the tree structure during the traversal. before visiting the left tree of a root, we will build a back-edge between a rightmost node in the left tree and the root. So we can go back to the root node after we are done with traversing the left tree.
Then we locate the rightmost node in the left subtree again, cut the back-edge, recover the tree structure, and start visit the right subtree.
The detection of incorrect tree nodes is similar to the recursion/iteration case.
Algorithm
- Perform Morris traversal and process each node in inorder fashion.
- For every node (except the leftmost node of the tree), keep track of its previous node in prev. The current node being processed is stored in the curr.
- If during the traversal, we find a node that violates the BST order. i.e. prev->data > root->data.we store prev into first and root into second.
- During further traversal, if we find another node that violates the BST criteria,i.e. prev->data > root->data. but since, the first node had been already assigned a value. so we assign the current node(which violates BST criteria) to second.
- After execution of inorder traversal. swap the data of first and second nodes and The tree gets fixed.

Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
// function that corrects the BST by performing iterative inorder
// and returns it's root
Node* fixBST(Node *root)
{
Node *prev,*first,*second;
prev = first = second = NULL;
// stores rightmost node in left subtree of root
Node* rightMost = NULL;
// stores current node starting with root node
Node* curr = root;
while(curr != NULL)
{
// for each node, we compare it with prev node as we did in in-order-traversal
if(prev != NULL && curr->data < prev->data)
{
if(first == NULL)
first = prev;
second = curr;
}
if(curr->left != NULL)
{
// got left tree, then let's locate its rightmost node in left tree
rightMost = curr->left;
// we may have visited the left tree before, and connect the rightmost node with curr node (root node)
while(rightMost->right != NULL && rightMost->right != curr)
rightMost = rightMost->right;
if(rightMost->right == curr)
{
// if this left tree has been visited before, then we are done with it
// cut the connection with currNode and start visit curr's right tree
rightMost->right = NULL;
prev = curr;
curr = curr->right;
}
else
{
// if this left tree has not been visited before, then we create a back edge from rightmost node
// to curr node, so we can return to the start point after done the left tree
rightMost->right = curr;
curr = curr->left;
}
}
else
{
// no left tree, then just visit its right tree
prev = curr;
curr = curr->right;
}
}
// swap the values of incorrect nodes
swap(first->data,second->data);
return root;
}
// function to simply perform inorder traversal of the tree
void inorder(Node *root)
{
if(root == NULL)
return;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
int main()
{
/* create the incorrect BST*/
Node *root = new Node(4);
root->left = new Node(7);
root->right = new Node(6);
root->left->left = new Node(1);
root->left->right = new Node(3);
root->right->left = new Node(5);
root->right->right = new Node(2);
cout<<"Inorder traversal before : ";
inorder(root);
root = fixBST(root);
cout<<endl;
cout<<"Inorder traversal after : ";
inorder(root);
return 0;
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
// function that corrects the BST using morris traversal and returns it's root
static Node fixBST(Node root)
{
Node prev,first,second;
prev = first = second = null;
// stores rightmost node in left subtree of root
Node rightMost = null;
// stores current node starting with root node
Node curr = root;
while(curr != null)
{
// for each node, we compare it with prev node as we did in in-order-traversal
if(prev != null && curr.data < prev.data)
{
if(first == null)
first = prev;
second = curr;
}
if(curr.left != null)
{
// got left tree, then let's locate its rightmost node in left tree
rightMost = curr.left;
// we may have visited the left tree before, and connect the rightmost node with curr node (root node)
while(rightMost.right != null && rightMost.right != curr)
rightMost = rightMost.right;
if(rightMost.right == curr)
{
// if this left tree has been visited before, then we are done with it
// cut the connection with currNode and start visit curr's right tree
rightMost.right = null;
prev = curr;
curr = curr.right;
}
else
{
// if this left tree has not been visited before, then we create a back edge from rightmost node
// to curr node, so we can return to the start point after done the left tree
rightMost.right = curr;
curr = curr.left;
}
}
else
{
// no left tree, then just visit its right tree
prev = curr;
curr = curr.right;
}
}
// swap the values of incorrect nodes
int temp = first.data;
first.data = second.data;
second.data = temp;
return root;
}
// function to simply perform inorder traversal of the tree
static void inorder(Node root)
{
if(root == null)
return;
inorder(root.left);
System.out.print(root.data+" ");
inorder(root.right);
}
public static void main (String[] args)
{
/* create the incorrect BST*/
Node root = new Node(4);
root.left = new Node(7);
root.right = new Node(6);
root.left.left = new Node(1);
root.left.right = new Node(3);
root.right.left = new Node(5);
root.right.right = new Node(2);
System.out.print("Inorder Traversal before : ");
inorder(root);
// fixing the BST
root = fixBST(root);
System.out.println();
System.out.print("Inorder Traversal after : ");
inorder(root);
}
}Inorder Traversal before : 1 7 3 4 5 6 2 Inorder Traversal after : 1 2 3 4 5 6 7
Complexity Analysis for Recover Binary Search Tree
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(1), nor data structure neither recursion stack space used.