Given a Binary Tree, connect nodes that are at the same level from left to right.
Structure of the Tree Node: A node of the tree contains 4 components which are data(integer value), pointers(next, left and right) of the tree node type. next pointer of a node point towards its right node at the same level. If the node is the rightmost node in that level then, it’s next pointer points to the null value. left and right pointers point to the left and right child respectively. The structure of a tree node is depicted below :

Table of Contents
Example
Input :
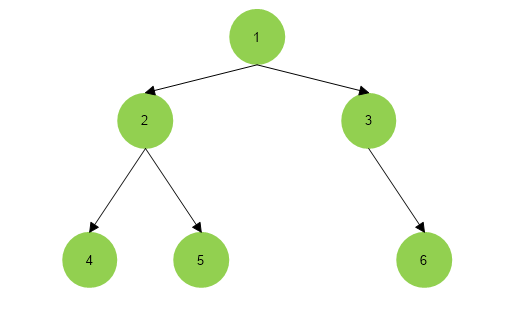
Output :
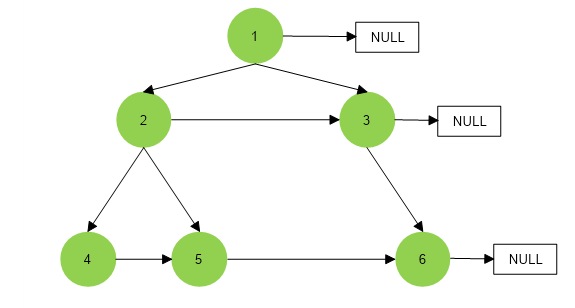
Input :
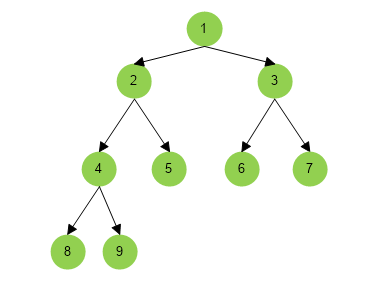
Output :
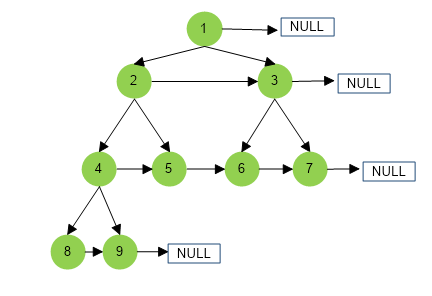
Input :

Output :
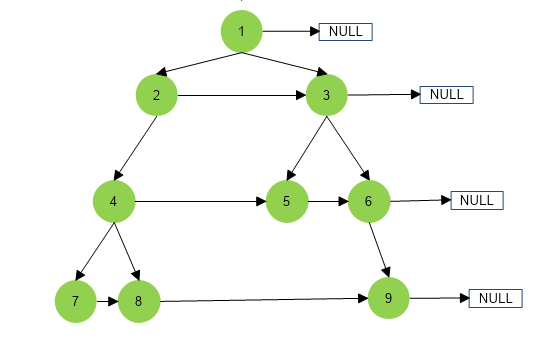
Explanation
- to connect two nodes a and b from left to right, you to make the following operation: a->next = b.
- Initially, the next pointers of all the tree nodes are set to null.
- Device an algorithm that sets the next pointer of each node to the next node (towards the right) at the same level.
- The next pointer of the rightmost node at each level is set to null.
Types of Solution
- Level order Traversal/Breadth First Search (BFS).
- Pre-order Traversal
- constant space – recursive
- constant space – iterative
Level order Traversal/BFS
Approach for Populating Next Right Pointers in Each Node
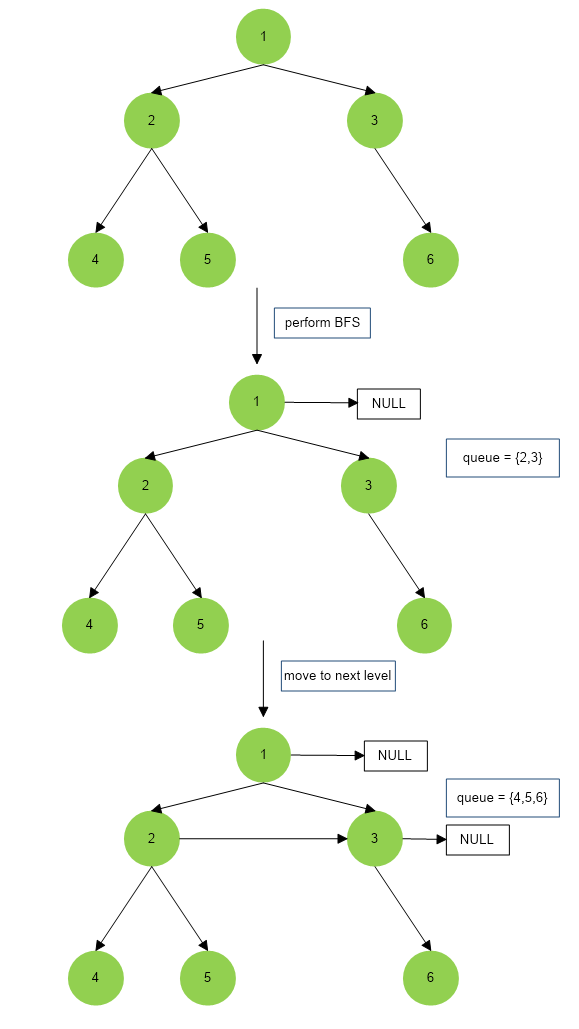
The idea is to perform BFS on the given binary tree, we use a queue that stores the nodes in level order way. In the queue, we store the nodes along with their level numbers. Once, we have stored all the nodes of a particular level, we simply pop them one by one and connect the previously popped nodes with the currently popped node using the next pointer. Also assure that, next of rightmost(last popped node of a level) node should point to null.
Algorithm
- Perform BFS on the given binary tree. While performing BFS on a tree, all the nodes on a particular level are pushed into the queue.
- Pop all the nodes at the same level (in the binary tree) from the queue one by one.
- While popping the nodes, assign the next pointer of the previous node to the current node.
- Perform steps 2 and 3 for every level of the binary tree.
The above algorithm is depicted below :
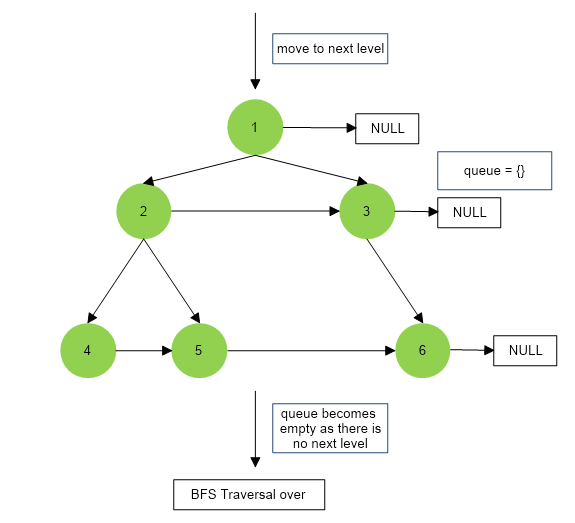
Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
// function that makes appropriate connections
void connect(Node *root)
{
// create queue to hold nodes at same level
queue <Node*> q;
// insert root node
q.push(root);
// used to store the current node
Node* temp = NULL;
while (!q.empty())
{
int n = q.size();
for (int i = 0; i < n; i++)
{
// previous stores last popped node from the queue
Node* prev = temp;
temp = q.front();
q.pop();
/*
when i = 0, prev is the first node of a level
so we have to skip this node.
and change next pointer from next node onwards
*/
if (i > 0)
prev->next = temp;
if (temp->left != NULL)
q.push(temp->left);
if (temp->right != NULL)
q.push(temp->right);
}
// pointing last node of a particular level to null
temp->next = NULL;
}
}
// Function to print node values of a particular level
void printLevel(Node* root)
{
if(root == NULL)
{
cout<<endl;
return;
}
cout<<root->data<<" ";
printLevel(root->next);
}
int main()
{
/* create the binary tree*/
Node *root = NULL;
root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->right = new Node(6);
connect(root);
cout<<"1st Level : ";
printLevel(root);
cout<<"2nd Level : ";
printLevel(root->left);
cout<<"3rd Level : ";
printLevel(root->left->left);
return 0;
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
// function that makes appropriate connections
static void connect(Node root)
{
// create queue to hold nodes at same level
Queue<Node> q = new LinkedList<>();
// insert root node
q.add(root);
// used to store the current node
Node temp = null;
while (!q.isEmpty())
{
int n = q.size();
for (int i = 0; i < n; i++)
{
// previous stores last popped node from the queue
Node prev = temp;
temp = q.poll();
/*
when i = 0, prev is the first node of a level
so we have to skip this node.
and change next pointer from next node onwards
*/
if (i > 0)
prev.next = temp;
if (temp.left != null)
q.add(temp.left);
if (temp.right != null)
q.add(temp.right);
}
// pointing last node of a particular level to null
temp.next = null;
}
}
// Function to print node values of a particular level
static void printLevel(Node root)
{
if(root == null)
{
System.out.println();
return;
}
System.out.print(root.data+" ");
printLevel(root.next);
}
// main Function to implement above function
public static void main (String[] args)
{
/* create the binary tree*/
Node root = null;
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
connect(root);
System.out.print("1st Level : ");
printLevel(root);
System.out.print("2nd Level : ");
printLevel(root.left);
System.out.print("3rd Level : ");
printLevel(root.left.left);
}
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6
Complexity Analysis for Populating Next Right Pointers in Each Node
- Time Complexity: T(n) = O(n), each node of the tree is processed.
- Space Complexity : A(n) = O(n).
Pre-order Traversal
Approach for Populating Next Right Pointers in Each Node
This method works only for complete binary trees.
Complete Binary Trees: A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. Below is an example of a complete binary tree.

Below is an example of the not complete binary tree.

The idea is to assign the next pointer of each node in a pre-order fashion, i.e. next of parent nodes is assigned before next of children nodes.
Since the given tree is a complete binary tree, we can make the following statements :
- For a parent node par, next of the left child of par would be the right child of par. i.e. par->left->next = par->right.
- next of right child of par would be left child of next of par. i.e. par->right->next = par->next->left.
- right child of a rightmost parent in the tree would be null. i.e. par->right->next = null (if par is rightmost parent).
After making the above observations, we can design a recursive pre-order (processing parents before children) algorithm that is able to assign the next pointers of all the nodes in the tree.
Algorithm
- Define base case.
- Assign next of left children of parent node to right children of par, i.e. par->left->next = par->right.
- Assign next of right children of parent node to left children par->next. i.e. par->right->next = par->next->left.
- Recursively perform steps 2 and 3 for the left and right children of the parent node.
The above algorithm is depicted below :


Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
/*a utility function to Set next pointers of all descendents of par node
and recursively perform the same for left and right child of par (Preorder traversal)*/
void utility(Node* par)
{
// define base case
if (!par)
return;
// set next pointer of par's left child
if (par->left)
par->left->next = par->right;
/* set next pointer of par's right child
as per the method discussed above */
if (par->right)
par->right->next = (par->next) ? par->next->left : NULL;
/* recursively set next of children nodes
in a preorder fashion*/
utility(par->left);
utility(par->right);
}
/* function that sets next pointers of
nodes in the tree using utility function*/
void connect(Node *root)
{
if(!root)
return;
root->next = NULL;
utility(root);
}
// Function to print node values of a particular level
void printLevel(Node* root)
{
if(root == NULL)
{
cout<<endl;
return;
}
cout<<root->data<<" ";
printLevel(root->next);
}
int main()
{
/* create the binary tree*/
Node *root = NULL;
/* for above algorithm to work properly
we have to construct a complete binary tree */
root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
root->left->left->left = new Node(8);
root->left->left->right = new Node(9);
connect(root);
cout<<"1st Level : ";
printLevel(root);
cout<<"2nd Level : ";
printLevel(root->left);
cout<<"3rd Level : ";
printLevel(root->left->left);
cout<<"4th Level : ";
printLevel(root->left->left->left);
return 0;
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 7 4th Level : 8 9
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
/*a utility function to Set next pointers of all descendents of par node
and recursively perform the same for left and right child of par (Preorder traversal)*/
static void utility(Node par)
{
// define base case
if (par == null)
return;
// set next pointer of par's left child
if (par.left != null)
par.left.next = par.right;
/* set next pointer of par's right child
as per the method discussed above */
if (par.right != null)
par.right.next = (par.next != null)? par.next.left : null;
/* recursively set next of children nodes
in a preorder fashion*/
utility(par.left);
utility(par.right);
}
/* function that sets next pointers of
nodes in the tree using utility function*/
static void connect(Node root)
{
if(root == null)
return;
root.next = null;
utility(root);
}
// Function to print node values of a particular level
static void printLevel(Node root)
{
if(root == null)
{
System.out.println();
return;
}
System.out.print(root.data+" ");
printLevel(root.next);
}
// main Function to implement above function
public static void main (String[] args)
{
/* create the binary tree*/
Node root = null;
/* for above algorithm to work properly we have to construct a complete binary tree */
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.left.left.left = new Node(8);
root.left.left.right = new Node(9);
connect(root);
System.out.print("1st Level : ");
printLevel(root);
System.out.print("2nd Level : ");
printLevel(root.left);
System.out.print("3rd Level : ");
printLevel(root.left.left);
System.out.print("4th Level : ");
printLevel(root.left.left.left);
}
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 7 4th Level : 8 9
Complexity Analysis for Populating Next Right Pointers in Each Node
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(1)
Recursive
Approach for Populating Next Right Pointers in Each Node
This approach is similar to the previous approach, but with some minor modifications to the code, we can make it work for all kinds of binary trees (whether complete or not).
The idea is to basically ensure that all the nodes on level i have their next pointers set before the nodes of (i+1)th level. We can achieve this by performing in order(parent before children) traversal but with a slight modification.
We traverse the nodes in the following order : (parent, next-right of a parent, left child, right child).
In this way, all the nodes at the i-th level are set before the nodes of (i+1)th level.
Now we can follow the steps below to achieve our objective :
- When we have set the next pointer of the left child of the parent node, we check whether the right child of the parent is present or not.
- If the right child is present, we simply set next of left child to right. i.e. par->left->next = par->right.
- Else, we use a function nextRight() that basically returns the address of first node just to the right of the left child & simply assign next of left to the node returned. i.e. par->left->next = nextRight(par).
- nextRight() uses the parent node (par) and it’s next pointer (par->next), to look for the first non-leaf (and return address of its child – left/right, whichever present) node towards right in the same level.
- For the right child of the parent node, we simply use the nextRight() function to return the address of the node just towards the right of the right child at the same level and assign it’s next pointer to the returned address. i.e. par->right->next = nextRight().
- If the node to the right of the current node at the same level is not present, we simply return null.
Algorithm
- Consider the current node as the parent node and all the next pointers in the current level have already been set.
- Consider left child of the parent node(if it exists) :
- If right child exists, Assign next of left child to right child of parent. i.e. par->left->next = par->right.
- Else, find the next node on the same level, and assign it to next of the left child, i.e. par->left = nextRight(par).
- Recursively Perform the above 2 steps for next of left child.(i.e. par->left->next).
- In this way, all the nodes on the same level have been set.
- If the left doesn’t exist, then consider the right child of the parent node.
- find the next node on the same level and assign it to next of right child, i.e. par->right = nextRight(par).
- Recursively Perform the steps 2.1 and 2.2 for next of right child.(i.e. par->right->next).
- In this way, all the nodes on the same level have been set.
- If both the child doesn’t exist, then recur to next of the parent node.(i.e. par->next).
The above algorithm is depicted below :

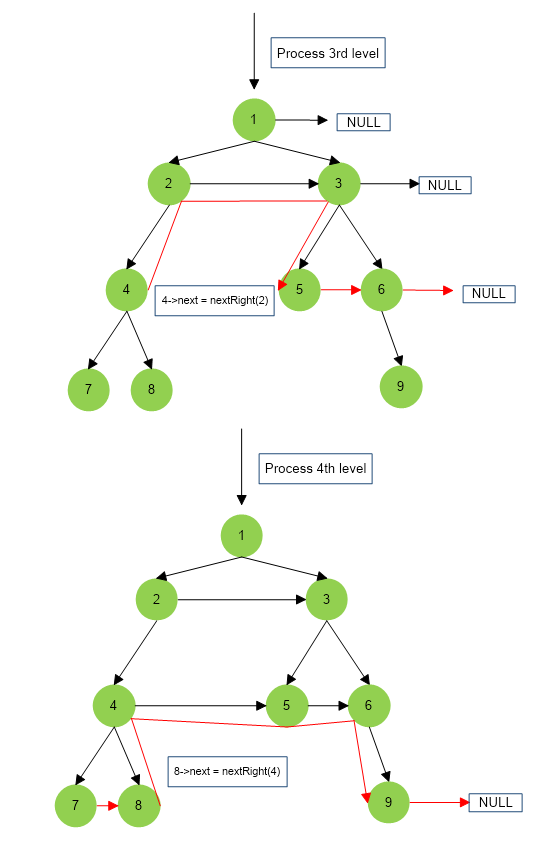

Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
/* This function is used to get first pointer just to the right of children of par */
Node* nextRight(Node *par)
{
// start traversing nodes on the same level with par towards the right
Node* temp = par->next;
// move to right until a node with atleast one children is found
while(temp != NULL)
{
// return the first children of node to the right
if(temp->left != NULL)
return temp->left;
if(temp->right != NULL)
return temp->right;
// if node to the right has no children. Then,
// move to next node to the right on same level
temp = temp->next;
}
// If all the nodes at par level are leaf nodes then return null
return NULL;
}
// function to recursively set next of all children of parent node par
// It ensures that nodes at ith level are set before those at (i+1)th level
void utility(Node* par)
{
// base case
if (!par)
return;
/* before setting next pointers of children,
set next pointers of par and the nodes at the same level as par
*/
if (par->next != NULL)
utility(par->next);
/* Set the next pointer for par's left child */
if (par->left)
{
if (par->right)
{
par->left->next = par->right;
par->right->next = nextRight(par);
}
else
par->left->next = nextRight(par);
/* recursively call for next level nodes,
the call for left child would automatically call
all it's right child */
utility(par->left);
}
/* If left child is null then first node of next level is the right child */
else if (par->right)
{
par->right->next = nextRight(par);
utility(par->right);
}
/* if both the children of parent node are null,
then we move on to next node in the same level*/
else
utility(nextRight(par));
}
/* function that sets next pointers of
nodes in the tree using utility function*/
void connect(Node *root)
{
if(!root)
return;
root->next = NULL;
utility(root);
}
// Function to print node values of a particular level
void printLevel(Node* root)
{
if(!root)
{
cout<<endl;
return;
}
cout<<root->data<<" ";
printLevel(root->next);
}
int main()
{
/* construct the binary tree */
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->left->left->left = new Node(7);
root->left->left->right = new Node(8);
root->right->right->right = new Node(9);
connect(root);
cout<<"1st Level : ";
printLevel(root);
cout<<"2nd Level : ";
printLevel(root->left);
cout<<"3rd Level : ";
printLevel(root->left->left);
cout<<"4th Level : ";
printLevel(root->left->left->left);
return 0;
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 4th Level : 7 8 9
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
/* This function is used to get first pointer just to the right of children of par */
static Node nextRight(Node par)
{
// start traversing nodes on the same level with par towards the right
Node temp = par.next;
// move to right until a node with atleast one children is found
while(temp != null)
{
// return the first children of node to the right
if(temp.left != null)
return temp.left;
if(temp.right != null)
return temp.right;
// if node to the right has no children. Then,
// move to next node to the right on same level
temp = temp.next;
}
// If all the nodes at par level are leaf nodes then return null
return null;
}
// function to recursively set next of all children of parent node par
// It ensures that nodes at ith level are set before those at (i+1)th level
static void utility(Node par)
{
// base case
if (par == null)
return;
/*
before setting next pointers of children,
set next pointers of par and the nodes at the same level as par
*/
if (par.next != null)
utility(par.next);
/* Set the next pointer for par's left child */
if (par.left != null)
{
if (par.right != null)
{
par.left.next = par.right;
par.right.next = nextRight(par);
}
else
par.left.next = nextRight(par);
/* recursively call for next level nodes,
the call for left child would automatically call
all it's right child */
utility(par.left);
}
/* If left child is null then first node of next level is the right child */
else if (par.right != null)
{
par.right.next = nextRight(par);
utility(par.right);
}
/* if both the children of parent node are null,
then we move on to next node in the same level*/
else
utility(nextRight(par));
}
/* function that sets next pointers of
nodes in the tree using utility function*/
static void connect(Node root)
{
if(root == null)
return;
root.next = null;
utility(root);
}
// Function to print node values of a particular level
static void printLevel(Node root)
{
if(root == null)
{
System.out.println();
return;
}
System.out.print(root.data+" ");
printLevel(root.next);
}
// main Function to implement above function
public static void main (String[] args)
{
/* construct the binary tree */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.right.left = new Node(5);
root.right.right = new Node(6);
root.left.left.left = new Node(7);
root.left.left.right = new Node(8);
root.right.right.right = new Node(9);
connect(root);
System.out.print("1st Level : ");
printLevel(root);
System.out.print("2nd Level : ");
printLevel(root.left);
System.out.print("3rd Level : ");
printLevel(root.left.left);
System.out.print("4th Level : ");
printLevel(root.left.left.left);
}
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 4th Level : 7 8 9
Complexity Analysis for Populating Next Right Pointers in Each Node
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(1)
Iterative
Approach for Populating Next Right Pointers in Each Node
The idea is to convert the above recursive code into an iterative code. The code consists of two nested while loops. The outer loop is used to move down through the tree levels(or generations) and the inner loop is used to traverse all the nodes on a particular level. Once we have dealt with all the nodes on a particular level, we move down to the next level.
The idea is to basically ensure that all the nodes on level i have their next pointers set before the nodes of (i+1)th level. We can achieve this by performing in order(parent before children) traversal but with a slight modification.
We traverse the nodes in the following order : (parent, next-right of a parent, left child, right child).
In this way, all the nodes at the i-th level are set before the nodes of (i+1)th level.
Now we can follow the steps below to achieve our objective :
- When we have set the next pointer of left child of parent node, we check whether right child of the parent is present or not.
- If the right child is present, we simply set next of left child to right. i.e. par->left->next = par->right.
- Else, we use a function nextRight() that basically returns the address of first node just to the right of the left child & simply assign next of left to the node returned. i.e. par->left->next = nextRight(par).
- nextRight() uses the parent node (par) and it’s next pointer (par->next), to look for the first non-leaf (and return address of its child – left/right, whichever present) node towards right in the same level.
- For the right child of the parent node, we simply use the nextRight() function to return the address of the node just towards the right of the right child at the same level and assign it’s next pointer to the returned address. i.e. par->right->next = nextRight().
- If the node to the right of the current node at the same level is not present, we simply return null.
Algorithm
- Consider the current node as the parent node and all the next pointers in the current level have already been set.
- Consider left child of the parent node(if it exists) :
- If right child exists, Assign next of left child to right child of parent. i.e. par->left->next = par->right.
- Else, find the next node on the same level, and assign it to next of the left child, i.e. par->left = nextRight(par).
- Iteratively Perform the above 2 steps for next of left child.(i.e. par->left->next).
- In this way, all the nodes on the same level have been set.
- If the left doesn’t exist, then consider the right child of parent node.
- find the next node on the same level and assign it to next of right child, i.e. par->right = nextRight(par).
- Iteratively Perform the steps 2.1 and 2.2 for next of right child.(i.e. par->right->next).
- In this way, all the nodes on the same level have been set.
- If both the child doesn’t exist, then Iterate to next of the parent node.(i.e. par->next).
The above algorithm is depicted below :



Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// blueprint of the tree node
class Node
{
public :
int data;
Node *left, *right, *next;
Node(int key)
{
data = key;
left = right = next = NULL;
}
};
/* This function is used to get first pointer just to the right of children of par */
Node* nextRight(Node *par)
{
// start traversing nodes on the same level with par towards the right
Node* temp = par->next;
// move to right until a node with atleast one children is found
while(temp != NULL)
{
// return the first children of node to the right
if(temp->left != NULL)
return temp->left;
if(temp->right != NULL)
return temp->right;
// if node to the right has no children. Then,
// move to next node to the right on same level
temp = temp->next;
}
// If all the nodes at par level are leaf nodes then return null
return NULL;
}
// function to Iteratively set next of all children of parent node par
// It ensures that nodes at ith level are set before those at (i+1)th level
void connect(Node *root)
{
if (!root)
return;
// set next for root
root->next = NULL;
// set next of all nodes in the current level
// after which Iterate to next level
while (root != NULL)
{
Node* par = root;
/* Connect all childrem nodes of par and
children nodes of all other nodes at
same level as par */
while (par != NULL)
{
// set the next pointer for par's left child
if (par->left)
{
if (par->right)
par->left->next = par->right;
else
par->left->next = nextRight(par);
}
// set next for par's right children
if (par->right)
par->right->next = nextRight(par);
// set next of all the nodes on the same level as children of par
par = par->next;
}
// After processing all the nodes of current Level
// move down to next level
if (root->left)
root = root->left;
else if (root->right)
root = root->right;
else
root = nextRight(root);
}
}
// Function to print node values of a particular level
void printLevel(Node* root)
{
if(!root)
{
cout<<endl;
return;
}
cout<<root->data<<" ";
printLevel(root->next);
}
int main()
{
/* construct the binary tree */
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->left->left->left = new Node(7);
root->left->left->right = new Node(8);
root->right->right->right = new Node(9);
connect(root);
cout<<"1st Level : ";
printLevel(root);
cout<<"2nd Level : ";
printLevel(root->left);
cout<<"3rd Level : ";
printLevel(root->left->left);
cout<<"4th Level : ";
printLevel(root->left->left->left);
return 0;
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 4th Level : 7 8 9
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
// blueprint of the tree node
static class Node
{
int data;
Node left, right, next;
Node(int key)
{
data = key;
left = right = next = null;
}
}
/* This function is used to get first pointer just to the right of children of par */
static Node nextRight(Node par)
{
// start traversing nodes on the same level with par towards the right
Node temp = par.next;
// move to right until a node with atleast one children is found
while(temp != null)
{
// return the first children of node to the right
if(temp.left != null)
return temp.left;
if(temp.right != null)
return temp.right;
// if node to the right has no children. Then,
// move to next node to the right on same level
temp = temp.next;
}
// If all the nodes at par level are leaf nodes then return null
return null;
}
// function to Iteratively set next of all children of parent node par
// It ensures that nodes at ith level are set before those at (i+1)th level
static void connect(Node root)
{
if (root == null)
return;
// set next for root
root.next = null;
// set next of all nodes in the current level
// after which Iterate to next level
while (root != null)
{
Node par = root;
/* Connect all children nodes of par and
children nodes of all other nodes at
same level as par */
while (par != null)
{
// set the next pointer for par's left child
if (par.left != null)
{
if (par.right != null)
par.left.next = par.right;
else
par.left.next = nextRight(par);
}
// set next for par's right children
if (par.right != null)
par.right.next = nextRight(par);
// set next of all the nodes on the same level as children of par
par = par.next;
}
// After processing all the nodes of current Level
// move down to next level
if (root.left != null)
root = root.left;
else if (root.right != null)
root = root.right;
else
root = nextRight(root);
}
}
// Function to print node values of a particular level
static void printLevel(Node root)
{
if(root == null)
{
System.out.println();
return;
}
System.out.print(root.data+" ");
printLevel(root.next);
}
// main Function to implement above function
public static void main (String[] args)
{
/* construct the binary tree */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.right.left = new Node(5);
root.right.right = new Node(6);
root.left.left.left = new Node(7);
root.left.left.right = new Node(8);
root.right.right.right = new Node(9);
connect(root);
System.out.print("1st Level : ");
printLevel(root);
System.out.print("2nd Level : ");
printLevel(root.left);
System.out.print("3rd Level : ");
printLevel(root.left.left);
System.out.print("4th Level : ");
printLevel(root.left.left.left);
}
}1st Level : 1 2nd Level : 2 3 3rd Level : 4 5 6 4th Level : 7 8 9
Complexity Analysis for Populating Next Right Pointers in Each Node
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(1)