The top view of a binary tree is the set of nodes visible when the tree is viewed from the top. Given a binary tree, the Output top view of the binary tree from the left-most horizontal level to the rightmost horizontal level.
Table of Contents
Example
Example 1
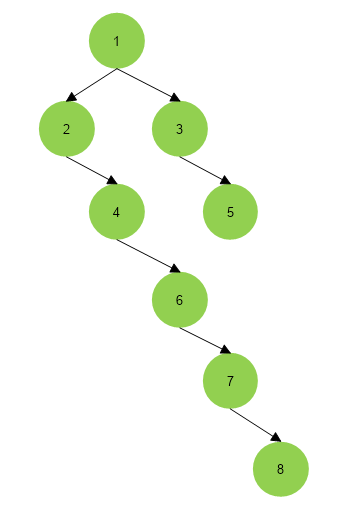
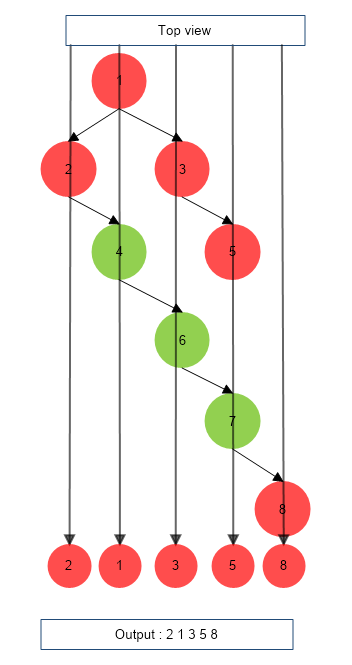
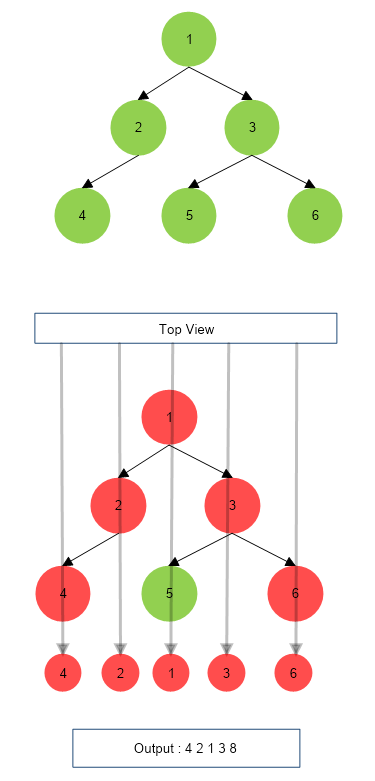
Example 2
Types of solution for Top View of Binary Tree
- DFS
- BFS
Depth First Search (DFS) / Inorder Traversal
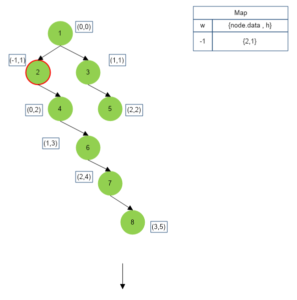
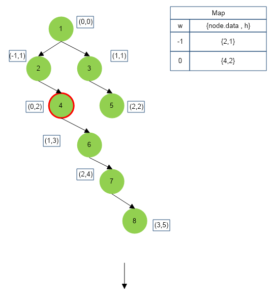
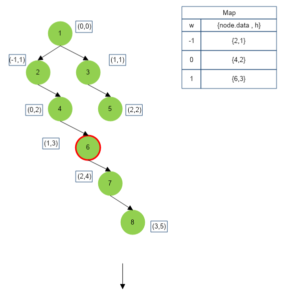
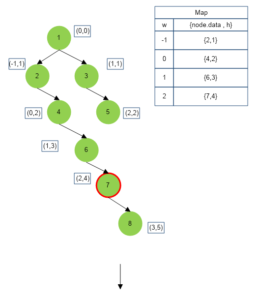
Approach for Top View of Binary Tree
We perform inorder traversal of the binary tree and keep track of vertical height(h) and horizontal width(w) of each node met during the traversal.
- If a particular horizontal width level has been visited for the first time, then we map this horizontal level (w value of that node) to node data (store the node in top view) and vertical height of that node. i.e. Map[horizontal width -> (node.data,vertical height)].
- If a particular horizontal width level has been visited already, then we check the vertical height (h value of that node) mapped for that horizontal width. If the vertical height of a current node is less than mapped vertical height (this happens when current node lies vertically above the previously mapped node and therefore appears in the top view of the tree superimposing over the previously mapped node) then we simply change mapped value of current horizontal width to {current node data, current node horizontal height}.
- After the traversal is over, simply output the top view node values in order of their horizontal levels.
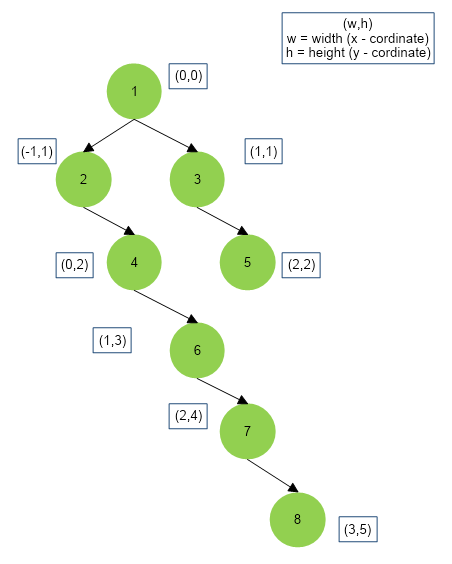
Below we depict the {horizontal width, vertical height} for each node of the binary tree :
Algorithm
- Create a map to store the top-view of the binary tree.
- Perform inorder traversal of the binary tree.
- During traversal keep track of vertical height(h) and horizontal width(w) of each of the tree nodes.
- For the node being visited currently, check if it’s horizontal width level has been visited or not.
- If the current horizontal level has not been visited then, map the {current horizontal width -> (current node data,current vertical height)}.
- If the current horizontal width level has been visited already then compare vertical height value already mapped for the current horizontal level with a vertical height of the current node.
- If the value of mapped vertical height is greater than the vertical height of current node (this happens when current node lies vertically above the previously mapped node and therefore appears in the top view of the tree superimposing over the previously mapped node) then, simply change the mapped value for current horizontal width to {current node data, current vertical height}. i.e. {current horizontal width -> (current node data,current vertical height)}.
- After the traversal, simply output the top view stored in the map.
The above algorithm is depicted below :

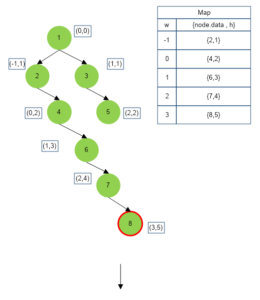

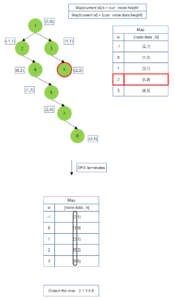
Implementation to print Top View of Binary Tree
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// defining the tree node
class Node
{
public :
int data;
Node *left;
Node *right;
// constructor for initialization
Node(int num)
{
data = num;
left = right = NULL;
}
};
/* the function performs inorder traversal and stores top view
of the binary tree.
for every node encountered during the traversal we have it's :
w -> horizontal depth(width)
h -> vertical depth(height)
*/
void inorder(Node *root,int w,int h, map<int,pair<int,int>> &Map)
{
if(root == NULL)
return;
inorder(root->left,w-1,h+1,Map);
/* check if a particular horizontal level has been visited or not */
if(Map.find(w) == Map.end())
Map[w] = make_pair(root->data,h);
/*
if particular horizontal level has been visited
then check if height of current node is less than
the previous node met at same horizontal level, if this
is true then the current node should replace previous node
in top view of the binary tree */
else if(Map[w].second>h)
Map[w] = make_pair(root->data,h);
inorder(root->right,w+1,h+1,Map);
}
/* function should print the topView of
the binary tree */
void topView(Node *root)
{
if(root == NULL)
return;
/* map to store node at each vertical(horizontal) distance(Level)
i.e. stores top view */
map<int,pair<int,int>> Map;
// obtain top view of binary tree into the Map
inorder(root,0,0,Map);
/* traverse the map and print top view */
for(auto i : Map)
cout<<i.second.first<<" ";
}
// main function to implement above functions
int main()
{
/* tree*/
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->right->right = new Node(5);
root->left->right = new Node(4);
root->left->right->right = new Node(6);
root->left->right->right->right = new Node(7);
root->left->right->right->right->right = new Node(8);
topView(root);
return 0;
}2 1 3 5 8
Java program
import java.io.*;
import java.util.*;
class tutorialCup
{
static class Node
{
int data;
Node left;
Node right;
Node(int num)
{
data = num;
left = right = null;
}
};
// class definition to handle pairs
static class pair
{
int nodeData;
int height;
pair(int key,int num)
{
nodeData = key;
height = num;
}
}
/* the function performs inorder traversal and stores top view
of the binary tree.
for every node encountered during the traversal we have it's :
w -> horizontal depth(width)
h -> vertical depth(height)
*/
static void inorder(Node root,int w,int h, TreeMap <Integer,pair> Map)
{
if(root == null)
return;
inorder(root.left,w-1,h+1,Map);
/* check if a particular horizontal level has been visited or not */
if(!Map.containsKey(w))
Map.put(w,new pair(root.data,h));
/* if particular horizontal level has been visited
then check if height of current node is less than
the previous node met at same horizontal level, if this
is true then the current node should replace previous node
in top view of the binary tree */
else if(Map.get(w).height > h)
Map.put(w,new pair(root.data,h));
inorder(root.right,w+1,h+1,Map);
}
/* function should print the topView of
the binary tree */
static void topView(Node root)
{
if(root == null)
return;
/* map to store node at each vertical(horizontal) distance(Level)
i.e. stores top view */
TreeMap<Integer,pair> Map = new TreeMap<>();
// obtain top view of binary tree into the Map
inorder(root,0,0,Map);
/* traverse the map and print top view */
for (Map.Entry<Integer, pair> i : Map.entrySet())
System.out.print(i.getValue().nodeData+" ");
}
/* main function to implement above function */
public static void main (String[] args)
{
/* construct the binary tree */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.right.right = new Node(5);
root.left.right = new Node(4);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);
root.left.right.right.right.right = new Node(8);
topView(root);
}
}2 1 3 5 8
Complexity Analysis for Top View of Binary Tree
- Time Complexity : T(n) = O(n)
- Space Complexity: A(n) = O(n), worst case is obtained when the tree is skewed.
Breadth first search(BFS) / Level order traversal
Approach for Top View of Binary Tree
We perform BFS of the binary tree. The idea behind this approach is that during BFS, a particular horizontal level of the tree is traversed before all the horizontal levels below so, we don’t have to keep track of vertical heights of each of the tree nodes. We simply track the horizontal depth/width of each of the tree nodes.
We perform the BFS traversal of the tree. During Traversal, if the horizontal width of the current node has not been visited then we simply map the current horizontal level to current node data. i.e. {current horizontal level -> current node data}. This mapping is stored in a treemap. At the end of the traversal, we simply output the top view stored in the map.
Below we depict the {horizontal width, vertical height} for each node of the binary tree :
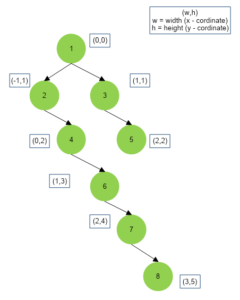
Algorithm
- Create a queue that stores nodes and their corresponding horizontal widths for BFS traversal.
- Create a map that stores the top view of the binary tree where the key is horizontal width and mapped value is node data.
- Perform the BFS traversal of the given binary tree.
- For the node being visited currently, check if it’s horizontal width has been visited already or not.
- If it’s horizontal width is being visited for the first time, then simply map the current horizontal width to current node data.
- After traversal, output the top view stored in the map.
The above algorithm is depicted below :









Implementation for Top View of Binary Tree
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// defining the tree node
class Node
{
public :
int data;
Node *left;
Node *right;
// constructor for initialization
Node(int num)
{
data = num;
left = right = NULL;
}
};
// function to obtain top-view of the binary tree
void topView(Node *root)
{
if(root == NULL)
return;
/* map to store node at each vertical(horizontal) distance(Level)
i.e. stores top view */
map<int,int> Map;
queue<pair<Node*,int>> q;
q.push({root,0});
// obtain top view of binary tree into the Map
while(!q.empty())
{
auto top = q.front();
q.pop();
Node *curr = top.first;
int horizontalLevel = top.second;
/* if the current horizontal Level has not been
visited then the first node encountered at this horizontal
level during level order traversal should be displayed
in top view of the tree */
if(Map.find(horizontalLevel) == Map.end())
Map[horizontalLevel] = curr->data;
if(curr->left)
q.push({curr->left,horizontalLevel-1});
if(curr->right)
q.push({curr->right,horizontalLevel+1});
}
// print the top view in order of horizontal Level
for(auto i : Map)
cout<<i.second<<" ";
}
// main function to implement above functions
int main()
{
/* construct the binary tree*/
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->right->right = new Node(5);
root->left->right = new Node(4);
root->left->right->right = new Node(6);
root->left->right->right->right = new Node(7);
root->left->right->right->right->right = new Node(8);
topView(root);
return 0;
}2 1 3 5 8
Java program
import java.io.*;
import java.util.*;
class tutorialCup
{
static class Node
{
int data;
Node left;
Node right;
Node(int num)
{
data = num;
left = right = null;
}
};
// class definition to handle pairs
static class pair
{
int nodeData;
int height;
pair(int key,int num)
{
nodeData = key;
height = num;
}
}
/* the function performs inorder traversal and stores top view
of the binary tree.
for every node encountered during the traversal we have it's :
w -> horizontal depth(width)
h -> vertical depth(height)
*/
static void inorder(Node root,int w,int h, TreeMap <Integer,pair> Map)
{
if(root == null)
return;
inorder(root.left,w-1,h+1,Map);
/* check if a particular horizontal level has been visited or not */
if(!Map.containsKey(w))
Map.put(w,new pair(root.data,h));
/* if particular horizontal level has been visited
then check if height of current node is less than
the previous node met at same horizontal level, if this
is true then the current node should replace previous node
in top view of the binary tree */
else if(Map.get(w).height > h)
Map.put(w,new pair(root.data,h));
inorder(root.right,w+1,h+1,Map);
}
/* function should print the topView of
the binary tree */
static void topView(Node root)
{
if(root == null)
return;
/* map to store node at each vertical(horizontal) distance(Level)
i.e. stores top view */
TreeMap<Integer,pair> Map = new TreeMap<>();
// obtain top view of binary tree into the Map
inorder(root,0,0,Map);
/* traverse the map and print top view */
for (Map.Entry<Integer, pair> i : Map.entrySet())
System.out.print(i.getValue().nodeData+" ");
}
/* main function to implement above function */
public static void main (String[] args)
{
/* construct the binary tree */
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.right.right = new Node(5);
root.left.right = new Node(4);
root.left.right.right = new Node(6);
root.left.right.right.right = new Node(7);
root.left.right.right.right.right = new Node(8);
topView(root);
}
}2 1 3 5 8
Complexity Analysis for Top View of Binary Tree
- Time Complexity: T(n) = O(n)
- Space Complexity: A(n) = O(n), worst case is obtained when the tree is skewed.