Red Black Tree is a self-balancing binary tree. In this tree, every node is either a red node or a black node. In this Red-black Tree Introduction, we will try to cover all of its basic properties.
Table of Contents
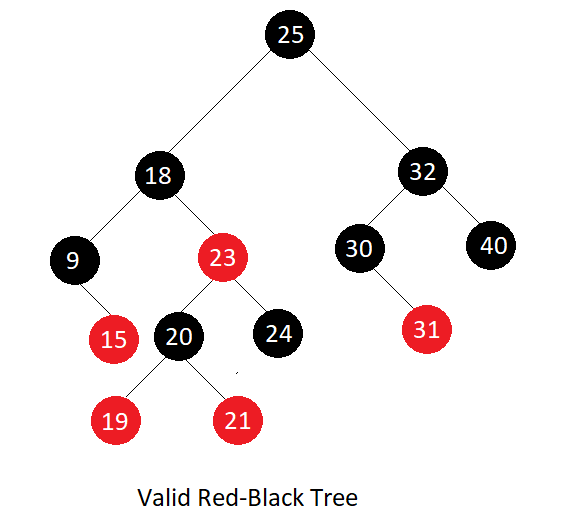
Properties of Red-Black Tree
- Every node is represented as either red or black.
- The root node is always black.
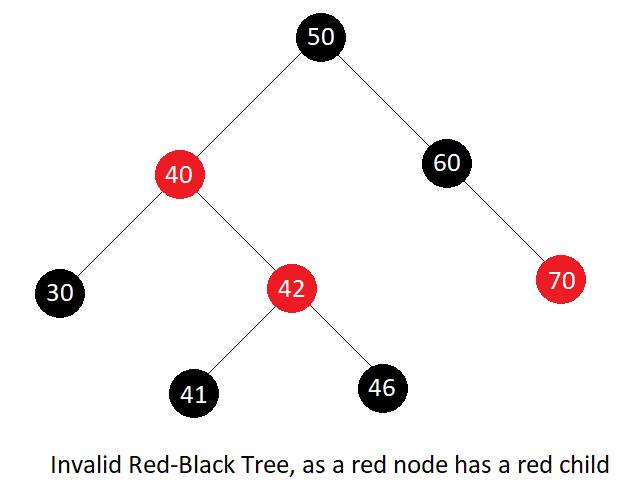
- A red node cannot have a red parent or a red child(i.e. no two red nodes are adjacent).
- Every path from any node to its NIL descendant must contain an equal number of black nodes.
Valid and Invalid examples of Red-Black Tree
Time Complexity Analysis
All the BST operations like searching, insertion, deletion, etc. can be performed in O(h) time, where h is the height of the red-black tree, and for a balanced BST the height is always of the order log(n) [n-> number of nodes].
Searching = O(log(n))
Insertion = O(log(n))
Deletion = O(log(n))
Black Height in Red-Black Tree
Black Height in a red-black tree is defined as the number of black nodes on the simple path (you do not visit same node twice) from any node to a leaf(which is NIL). It is represented by bh(x).
Height of Red-Black Tree
Unlike AVL tree, the height balance is not as strict, but in red-black trees, the number of rotations is less compared to that in AVL trees.
Height of a red-black tree h <= 2(log(n+1)) {Base of log is 2} Detailed proof of why the height of RB trees is <= 2 log (n+1).
To maintain the balance in height a red-black tree uses recoloring and restructuring.
You can see how the RB trees recolor and restructure themselves here.
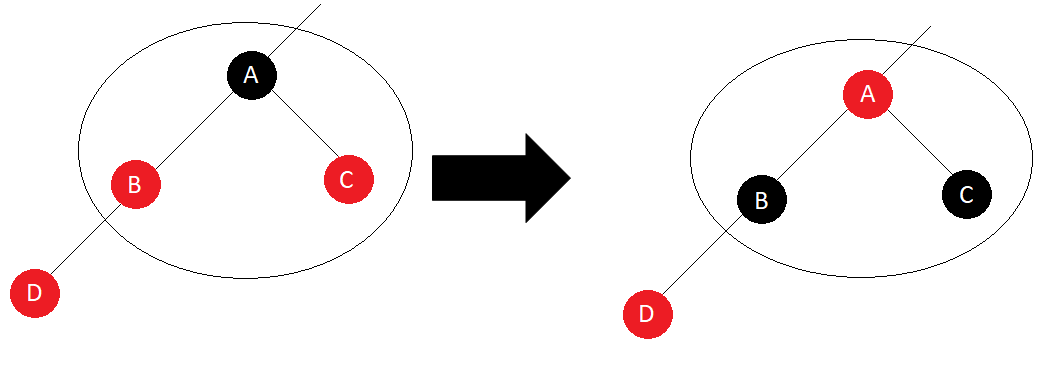
Recoloring
It refers to changing the color of some red nodes to black and vice-versa, it is done whenever the sibling of a red node’s red parent is red.
Restructuring
It refers to the rotation of the tree, it is done whenever a red child has a red parent and black or null uncle. There are four cases in restructuring,
- Right
- Left
- Right-Left
- Left-Right

Applications
- Used in real-world libraries to implement self-balancing BSTs.
- Used as TreeSet and TreeMap in JAVA and Sets and Maps in C++.
Searching
A red-black tree is a BST, so searching in an RBT is exactly the same as searching in BST, the color of the node does not matter.