Firstly we have to find the total number of counts to form a unique binary search tree. After it, we construct all possible unique BST. First of all, we have to know the construction of BST. In a Binary Search Tree, the nodes present in the left subtree wrt. any node in it is always less than the nodes on the right subtree. Let’s see the below diagrams of BST formed by N nodes(1 to N).
For N=3, we construct all possible unique BST’s form:
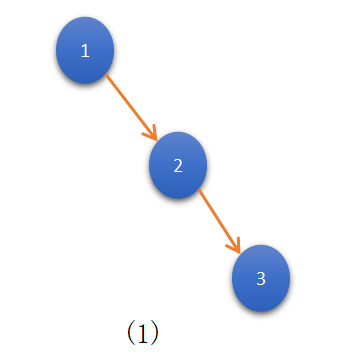
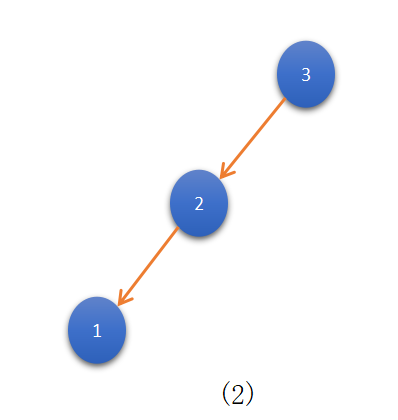
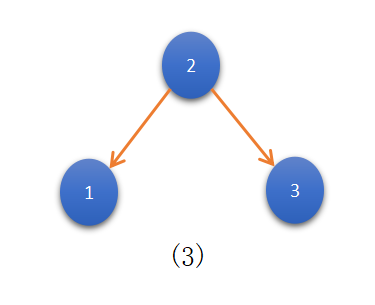


For N=3, we constructed 5 unique BST’s.
The total number of BST is equal to the product of the number of ways to choose root, number of left-subtrees, and number of right-subtrees.
We can find the number of BST’s using recursion:
- Choose 1 as root, no element present on left-subtree. N-1 elements present on the right subtree.
- Choose 2 as root, 1 element present on the left-subtree. N-2 elements present on the right-subtree.
- Similarly, Choose i as root, i-1 elements present on the left-subtree. N-i elements on the right-subtree.
Then, Total number of BST’s C(N) = C(0)*C(N-1) + C(1)*C(N-2) +………+ C(i-1)*C(N-i) +………….+ C(N-1)*C(0).
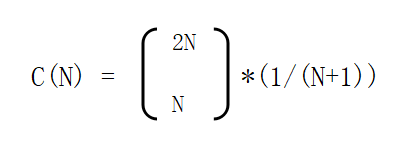
This formula is also called as Nth-Catalan Number.
Table of Contents
Implementation for finding Nth-Catalan Number
/*C++ Implementation for finding Nth-Catalan Number*/
#include<bits/stdc++.h>
using namespace std;
long long int ncr(long long int n, long long int r)
{
long long int res=1;
/*C(n,r)=C(n,n-r)*/
if(r>n-r)
{
r=n-r;
}
/*Calculate value of [n*(n-1)*---*(n-r+1)] / [r*(r-1)*---*1]*/
for(int i=0;i<r;i++)
{
res*=(n-i);
res/=(i+1);
}
return res;
}
/*Function which return Nth Catalan Number*/
long long int nth_catalan(int n)
{
/*Calculate value of 2nCn*/
long long int c=ncr(2*n,n);
/*return 2nCn/(n+1)*/
return c/(n+1);
}
int main()
{
int n;
/*input value*/
cin>>n;
cout<<nth_catalan(n)<<endl;
return 0;
}5
42
Time Complexity
O(N) which means, its complexity is linear. Iterate a single for loop for Calculate value of [n*(n-1)*—*(n-r+1)] / [r*(r-1)*—*1].
Algorithm
Algorithm:
Step:1 Create a list for storing the root of the BST.
Step:2 For i in range 1 to N:
i) Create a new node(temp) and assign its data as i.
ii) Construct list of all left subtrees using recursion.
iii) Construct list of all right subtrees using recursion.
Step:3 Traverse all left subtrees:
i) For the current left subtree, traverse all right subtrees.
ii) Add both left and right subtrees to temp.
iii) Add temp to the list.Implementation For Unique Binary Search Trees
/*C++ Implementation for Print the inorder traversal of all possible BST's by constructing them.*/
#include<bits/stdc++.h>
using namespace std;
struct node
{
int data;
struct node *left, *right;
};
/*create a Node*/
struct node *newNode(int item)
{
struct node *temp = new node;
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
void preorder(struct node *root)
{
if(root!=NULL)
{
cout<<root->data<<" ";
preorder(root->left);
preorder(root->right);
}
}
/*function for constructing BST's*/
vector<struct node *> bst(int start, int end)
{
vector<struct node *> list;
/*if start>end then subtree will be empty so returning NULL in the list */
if(start>end)
{
list.push_back(NULL);
return list;
}
/*iterating through all values from start to end for constructing left and right subtree recursively */
for(int i=start;i<=end;i++)
{
/* constructing left subtree */
vector<struct node *> leftSubtree = bst(start, i - 1);
/* constructing right subtree */
vector<struct node *> rightSubtree = bst(i + 1, end);
/* now looping through all left and right subtrees and connecting them to ith root below */
for(int j=0;j<leftSubtree.size();j++)
{
struct node* left = leftSubtree[j];
for(int k=0;k<rightSubtree.size();k++)
{
struct node* right = rightSubtree[k];
struct node* node = newNode(i);// making value i as root
node->left = left;// connect left subtree
node->right = right;// connect right subtree
list.push_back(node);// add this tree to list
}
}
}
return list;
}
int main()
{
int n;
/*input value*/
cin>>n;
/*construct all bst's*/
vector<struct node *> all_bst= bst(1,n);
cout<<"Printing Preorder traversal of all constructed BSTs are: "<<endl;
for(int i=0;i<all_bst.size();i++)
{
preorder(all_bst[i]);
cout<<endl;
}
return 0;
}5
Printing Preorder traversal of all constructed BSTs are: 1 2 3 4 5 1 2 3 5 4 1 2 4 3 5 1 2 5 3 4 1 2 5 4 3 1 3 2 4 5 1 3 2 5 4 1 4 2 3 5 1 4 3 2 5 1 5 2 3 4 1 5 2 4 3 1 5 3 2 4 1 5 4 2 3 1 5 4 3 2 2 1 3 4 5 2 1 3 5 4 2 1 4 3 5 2 1 5 3 4 2 1 5 4 3 3 1 2 4 5 3 1 2 5 4 3 2 1 4 5 3 2 1 5 4 4 1 2 3 5 4 1 3 2 5 4 2 1 3 5 4 3 1 2 5 4 3 2 1 5 5 1 2 3 4 5 1 2 4 3 5 1 3 2 4 5 1 4 2 3 5 1 4 3 2 5 2 1 3 4 5 2 1 4 3 5 3 1 2 4 5 3 2 1 4 5 4 1 2 3 5 4 1 3 2 5 4 2 1 3 5 4 3 1 2 5 4 3 2 1
Time complexity
O(N*V) where N is the number of nodes and V is the value of Nth Catalan number. We print the preorder traversal of all bst’s which is equal to nth Catalan number and we already aware that the time complexity of preorder traversal is O(N) where N number of nodes in BT.