Do we already know about what actually Binary Tree is? Now in this post, we are focusing on how to delete a node whose value is given. We are sure that the value of the node which we want to delete is always present before deletion in BT. In Binary Tree deletion, we use the concept of BFS traversal. The algorithm of the logic is as follow:
Algorithm
Step:1 Apply BFS on the given tree and it starts from root node.
Step:2 Print the level order traversal before deletion.
Step:3 Find the parent and data of the last node using BFS.
Step:4 Remove the last node.
Step:5 Once we find any node whose value is equal to the value of the node we want to remove then stop BFS.
Step:6 Replace the data of the present node and last node(rightmost) of the last level in BT.
Step:7 Print the level order traversal after deletion.
Let’s see quick understanding about deletion in BT:
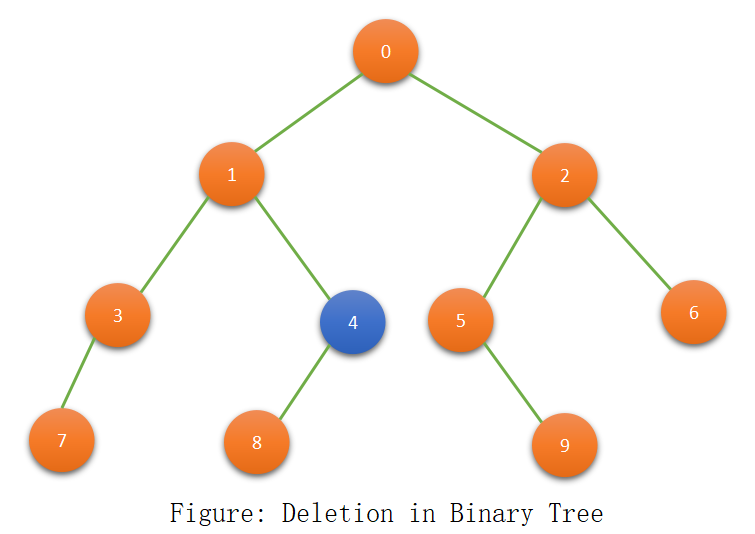
We want to delete a node with a value equal to 4. So we swap the value of the last node(9) with deleting node(4). After swapping delete the last node.
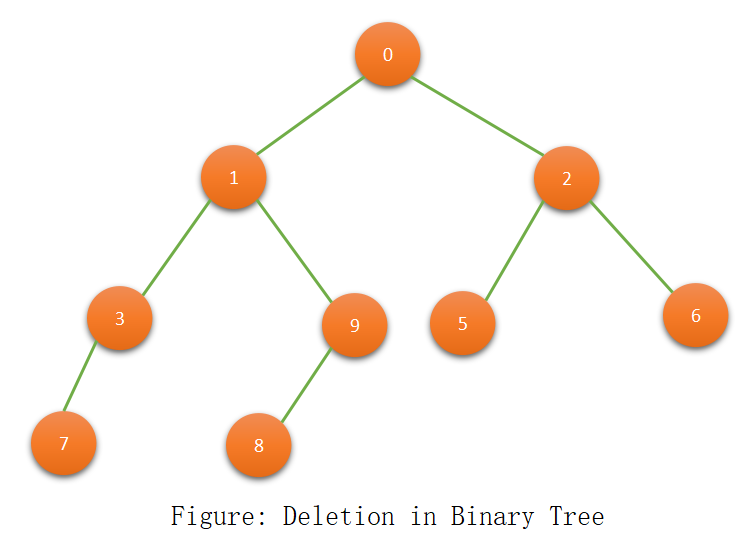
C++ Code for Deletion in a Binary Tree
/*C++ Implementation of Deletion in Binary Tree(Iterative Way)*/
#include<bits/stdc++.h>
using namespace std;
/*Structure of Node of BT which contain pointer to left child and right child and a data for node.*/
struct Node{
int data;
struct Node* left;// for left child;
struct Node* right;// for right child;
Node(int value)// create a node using new_Node;
{
data=value;
left=NULL;
right=NULL;
}
};
/*Function which print level order of the given tree*/
void level_order(Node* root)
{
if(root==NULL)
{
return;
}
queue<Node*> q;
q.push(root);
while(!q.empty())
{
Node* temp=q.front();
cout<<temp->data<<" ";
q.pop();
if(temp->left!=NULL)
{
q.push(temp->left);
}
if(temp->right!=NULL)
{
q.push(temp->right);
}
}
cout<<endl;
}
pair<Node*,int> last_node(Node* root)
{
if(root==NULL)
{
return make_pair(root,0);
}
queue<Node*> q;
q.push(root);
Node* last_parent=NULL;
int last_value;
while(!q.empty())
{
Node* temp=q.front();
/*store the parent of last node*/
if((temp->left!=NULL)&&(temp->right!=NULL))//if left and right sub tree are present;
{
if(temp->left->left==NULL&&temp->left->right==NULL&&temp->right->left==NULL&&temp->right->right==NULL)
{
last_parent=temp;
}
}
if(temp->left!=NULL)//if left subtree only present;
{
if(temp->left->left==NULL&&temp->left->right==NULL)
{
last_parent=temp;
}
}
if(temp->right!=NULL)//if right subtree only present;
{
if(temp->right->left==NULL&&temp->right->right==NULL)
{
last_parent=temp;
}
}
/*---------------end here---------------*/
/*for storing the value of last node.*/
last_value=temp->data;
q.pop();
if(temp->left!=NULL)
{
q.push(temp->left);
}
if(temp->right!=NULL)
{
q.push(temp->right);
}
}
/*return the parent of last node and the data of the last node*/
return make_pair(last_parent,last_value);
}
void delete_node(Node* root,int value,int last_value)
{
/*if only one node is present and we want to delete it*/
if(root->left==NULL&&root->right==NULL)
{
root=NULL;
return;
}
queue<Node*> q;
q.push(root);
while(!q.empty())
{
Node* temp=q.front();
q.pop();
/*if we find the node which we want to delete then change the data with last node data*/
if(temp->data==value)
{
temp->data=last_value;
}
if(temp->left!=NULL)
{
q.push(temp->left);
}
if(temp->right!=NULL)
{
q.push(temp->right);
}
}
}
int main()
{
/*construct tree*/
Node* root= new Node(0);//root node;
root->left= new Node(1);
root->right= new Node(2);
root->left->left= new Node(3);
root->left->right= new Node(4);
root->right->left= new Node(5);
root->right->right= new Node(6);
root->left->left->left= new Node(7);
root->left->right->left= new Node(8);
root->right->left->right= new Node(9);//last node
int value;
cin>>value;//input the data of node which we want to delete;
cout<<"Level order traversal before Deletion of node: ";
level_order(root);
/*Find the last node and its parent to remove last node from tree.*/
pair<Node*,int> last=last_node(root);
/*remove last node*/
if(last.first->left!=NULL&&last.first->left->data==last.second)
{
last.first->left=NULL;
}
if(last.first->right!=NULL&&last.first->right->data==last.second)
{
last.first->right=NULL;
}
/*delete the node*/
delete_node(root, value,last.second);
cout<<"Level order traversal after Deletion of node: ";
level_order(root);
return 0;
}4
Level order traversal before Deletion of node: 0 1 2 3 4 5 6 7 8 9 Level order traversal after Deletion of node: 0 1 2 3 9 5 6 7 8
Time Complexity
O(N) where N is the number of nodes in a binary tree.