Best Meeting Point LeetCode Solution

Difficulty Level Hard
Frequently asked in Amazon Bloomberg Expedia Facebook Google Microsoft Snapchat Twitter
Array Math Matrix Reddit SortingViews 1943

Problem Statement:

Best Meeting Point Leetcode Solution says – Given a m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance. The total travel distance is the sum of the distances between the houses of the friends and the meeting point. The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example:

Input:

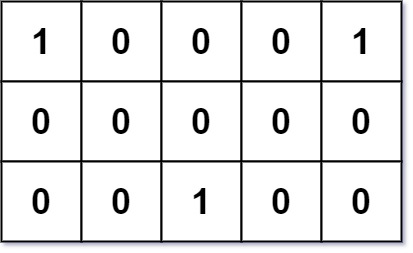
Best Meeting Point Leetcode Solution

 grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]

Output:

 6

Explanation:

Given three friends living at (0,0), (0,4), and (2,2). The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.

Approach:

Idea:

The idea is to select the coordinate closest to all the points in order to minimize the total distance. If we consider this problem only for a 1 dimension then the point i.e. closest to all the points turns out to be the median of the points. Now in the case of 2 dimensions, we need to consider the point which is median w.r.t both the dimensions. So we just need to calculate the median of the given points.

We first create 2 lists one for the x coordinates and another for the y coordinates for all the values where the value is 1. Now we will sort them and will take the median value from both the lists, say x_median and y_median. This (x_median,y_median) will be our meeting point. Finally, we calculate the Manhattan distance of all the friends from this median coordinate.

Code:

Best Meeting Point Leetcode C++ Solution:

class Solution {
public:
    int minTotalDistance(vector<vector<int>>& grid) {
        int friends=0;
        int n = grid.size();
        int m = grid[0].size();
        
        vector<int> x_cords;
        vector<int> y_cords;
        
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(grid[i][j]==1){
                    x_cords.push_back(i);
                    y_cords.push_back(j);
                    friends++;
                }
            }
        }
        
        sort(x_cords.begin(),x_cords.end());
        sort(y_cords.begin(),y_cords.end());
        
        int median_x = x_cords[friends/2];
        int median_y = y_cords[friends/2];
            
        int distance=0;
        for(int i=0;i<friends;i++){
            distance += abs(x_cords[i]-median_x) + abs(y_cords[i]-median_y);
        }
        return distance;
    }
};

Best Meeting Point Leetcode Python Solution

class Solution:
    def minTotalDistance(self, grid: List[List[int]]) -> int:
        friends=0;
        n = len(grid);
        m = len(grid[0]);
        
        x_cords = []
        y_cords = []
        
        for i in range(n):
            for j in range(m):
                if grid[i][j]==1:
                    x_cords.append(i)
                    y_cords.append(j)
                    friends+=1
        
        x_cords.sort();
        y_cords.sort();
        
        median_x = x_cords[friends//2]
        median_y = y_cords[friends//2]
            
        distance=0
        for i in range(friends):
            distance += abs(x_cords[i]-median_x) + abs(y_cords[i]-median_y)
        return distance

Complexity Analysis of Best Meeting Point Leetcode Solution:

  • Time Complexity: The time complexity of the above code is O(n*m) because we are traversing the entire grid.
  • Space Complexity: The space complexity of the above code is O(max(n,m)) because we are using a list to store the x and y coordinates.
Translate »