Minimum Path Sum Leetcode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg ByteDance Facebook Goldman Sachs Google Microsoft Oracle PayPal ServiceNow Snapchat Square Tesla Uber
Array Dynamic Programming MatrixViews 4500

Problem Statement

The Minimum Path Sum LeetCode Solution – “Minimum Path Sum” says that given a n x m grid consisting of non-negative integers and we need to find a path from top-left to bottom right, which minimizes the sum of all numbers along the path.

We can only move either down or right at any point in time.

Example:

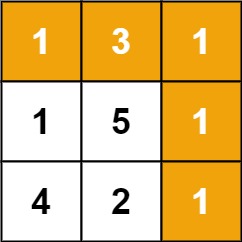
Minimum Path Sum Leetcode Solution

Input:  grid = [[1,3,1],[1,5,1],[4,2,1]]
Output:7

Explanation:

  • The optimal path that minimizes the sum from (0, 0) to (n – 1, m – 1) consists of the following cells.
  • (0, 0), (0, 1), (0, 2), (1, 2), (2, 2) and sum of all cells values in the minimum path is: 1 + 3 + 1 + 1 + 1 = 7
Input:  grid = [[1,2,3],[4,5,6]]
Output: 12

Explanation:

  • The Minimum Path Sum is 12 and the path corresponding to such value is: (0, 0), (0, 1), (0, 2), (1, 2).

Approach

Idea:

  1. The main idea to solve this problem is to use dynamic programming.
  2. To reach every cell (i, j), we can either come from the cell lying upwards (i – 1, j) or from the cell lying leftwards (i, j – 1).
  3. Iterate for each row and each column, and for every cell find the minimum of these two values:
    1. grid[i – 1][j] if (i – 1, j) exists otherwise INT_MAX.
    2. grid[i][j – 1] if (i, j – 1) exists otherwise INT_MAX.
  4. Hence, the minimum cost to reach the current cell will be grid[i][j] + min_value where min_value is the value obtained in the above step.
  5. Our answer will be grid[n – 1][m – 1].

Code

Minimum Path Sum Leetcode C++ Solution:

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[n - 1].size();
        for(int i=0; i<n; i++){
            for(int j=0; j<m; j++){
                int curr = INT_MAX;
                if(i - 1 >= 0)
                    curr = min(curr, grid[i - 1][j]);
                if(j - 1 >= 0)
                    curr = min(curr, grid[i][j - 1]);
                if(curr == INT_MAX)
                    curr = 0;
                grid[i][j] += curr;
            }
        }
        return grid[n - 1][m - 1];
    }
};

Minimum Path Sum Leetcode Java Solution:

class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length, m = grid[n - 1].length;
        for(int i=0; i<n; i++){
            for(int j=0; j<m; j++){
                int curr = Integer.MAX_VALUE;
                if(i - 1 >= 0){
                    curr = Math.min(curr, grid[i - 1][j]);
                }
                if(j - 1 >= 0){
                    curr = Math.min(curr, grid[i][j - 1]);
                }
                if(curr == Integer.MAX_VALUE){
                    curr = 0;
                }
                grid[i][j] += curr;
            }
        }
        
        return grid[n - 1][m - 1];
    }
}

Complexity Analysis for Minimum Path Sum Leetcode Solution

Time Complexity

The time complexity of the above code is O(N*M) since we’re iterating for each cell, where N = number of rows and M = number of columns.

Space Complexity

The space complexity of the above code is O(1) since we are using constant extra space.

Reference: https://en.wikipedia.org/wiki/Shortest_path_problem

Translate »