Table of Contents
Problem Statement
The Best Meeting Point LeetCode Solution says Given a binary grid grid of size m x n where each 1 determines the home of one friend, we want to return the minimal total travel distance where the total travel distance is the sum of the distances between the houses of the friends and the meeting point.
The total travel distance is calculated as the sum of Manhatten distance between the points.
Manhatten distance: The distance calculated as the sum of the absolute differences between the two vectors. i.e. Manhatten distance between points (x1,y1) and (x2,y2) can be calculated as:
D= | x1-x2| + |y1-y2|
In the above example :
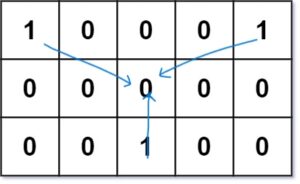
Input:
grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output:
6
Explanation:
Given are three friends located at positions (0,0), (0,4), and (2,2). The point (0,2) is an appropriate meeting point because the total travel distance is minimal i.e. 2 + 2 + 2 = 6. Hence, we return 6.
Another example :
Input:
grid = [[1,1]]
Output:
1
Solution Approach
The Concept
The point lying at the median coordinates (midx,midy) where midx is the median of x-coordinate values vector and midy is the median of the y-coordinate values vectoris the point of minimal Total travel distance.
Proof
Here in the graph,
Let a,b,c,d,e be five location points and x be a point of total travel distance Our goal is to find a location where the distance from all points to x i.e. D is minimum.
Case 1 : Let x lie at (0,0) D1= a+b+c+d+e
Case 2 : Let x lie before point a (closest to a) D2= (a-x)+(b-x)+(c-x)+(d-x)+(e-x) D2= a+b+c+d+e – 5*x D2= D1 -5*x => D2<D1 [ total travel distance in Case 2<Case 1]
Case 3 : Let x lie after point e (closest to e) D3= (x-a)+(x-b)+(x-c)+(x-d)+(x-e) D3= 5*x- a+b+c+d+e D3= 5*x – D1 [ Here x in Case 3 >>> x in Case 2] => D3>D2 [ total travel distance in Case 3>Case2]
Case 4 : Let x lie after point c (median point) D4= (c-a)+(c-b)+(c-c)+(d-c)+(e-c) D4= a+b+c+d+e – 5*c D4= a+b+d+e-4*c => D4<D2 [ Clearly, total travel distance in Case 2>Case3]
Clearly, considering the above 4 cases we can state that the total distance from all the points to the median is minimum.
Therefore, the Median point is the point of minimum Total travel Distance.
Approach
- Collect the x-coordinates of all positions with ‘1’ in a vector xcoordinates.
- Collect the y-coordinates of all positions with ‘1’ in a vector ycoordinates.
- Create a vector pair of all positions with ‘1’ distpoints.
- Sort xcoordinates and ycoordinates.
- Find median midx in xcoordinates and midy in ycoordinates [median = middle element in a sorted array, consider the first index of middle elements]
- Traverse through distpoints and add Manhatten distance through each point location to the median in total_travel_distance
- Return total_travel_distance.
Code
C++ Solution for Best Meeting Point LeetCode Solution
class Solution {
public:
int minTotalDistance(vector<vector<int>>& grid) {
vector<int>xcoordinates;
vector<int>ycoordinates;
//store pair of coordinate points
vector<pair<int,int>>distpoints;
// store all x-coordinates and y-coordinates in separate vectors O(nm)
for(int i=0;i<grid.size();i++){
for(int j=0;j<grid[i].size();j++){
if(grid[i][j]==1)
{
xcoordinates.push_back(i);
ycoordinates.push_back(j);
distpoints.push_back({i,j});
}
}
}
//sort both vectors O(nlogn)
sort(xcoordinates.begin(),xcoordinates.end());
sort(ycoordinates.begin(),ycoordinates.end());
//find mid element in both vectors [Median coordinates]
int index=0;
int midx=0;
int midy=0;
if (xcoordinates.size()%2==0)
index=xcoordinates.size()/2-1;
else
index=xcoordinates.size()/2;
midx= xcoordinates[index];
midy=ycoordinates[index];
//Find manhatten distance O(n)
int total_travel_distance=0;
for(int i=0;i<xcoordinates.size();i++){
total_travel_distance+=abs(distpoints[i].first-midx)+abs(distpoints[i].second-midy);
}
return total_travel_distance;
}
};Python Solution for Best Meeting Point LeetCode Solution
class Solution(object):
def minTotalDistance(self, grid):
colvals = []
rowvals = []
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
colvals.append(j)
rowvals.append(i)
colvals.sort()
rowvals.sort()
result = 0
total_travel_distance = (rowvals[len(rowvals)//2], colvals[len(colvals)//2])
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
result += abs(i-total_travel_distance[0]) + abs(j-total_travel_distance[1])
return result
Complexities for Best Meeting Point LeetCode Solution :
Time Complexity: O(mn), m, and n are numbers of rows and columns in the grid.
Space Complexity : O(p) , p=number of ‘1’s in grid
