Table of Contents
Problem Statement
The Word Ladder LeetCode Solution – “Word Ladder” states that you are given a string beginWord, string endWord, and a wordList.
We need to find the shortest transformation sequence length (if no path exists, print 0) from beginWord to endWord following the given conditions:
- All the Intermediate Words should be present in wordList.
- Every Consecutive Word in the shortest sequence should differ by exactly one character.
Example:
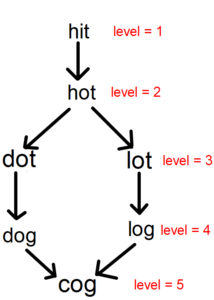
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation:
- Starts with the beginWord = “hit” (level=1).
- Words adjacent to “hit” and are not yet visited are “hot” since it differs only in 1 character. The level of “hot” is 2.
- Words adjacent to “hot” and are not yet visited are “dot” and “lot”. The level is 3.
- Words adjacent to “dot” and “lot” are “dog” and “log” respectively with level = 4.
- Words adjacent to dog and log is a cog, which is endWord, present at level = 5 which is our answer.
Input: beginWord = "hat", endWord = "lob", wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation:
- Since endWord “lob” doesn’t exist in the wordList, hence the output is 0[all intermediate words must exist in wordList].
Approach
Idea:
- Since we need to find the shortest path length from source to target, the key idea is to use Breadth-First Search (BFS) for a Graph.
- First, store all words from wordList to a set, to remove duplicate words.
- Perform BFS from beginWord and each time, pop out the front element string from the queue and visit all adjacent strings of current string(strings differing by one character and are present in wordList) push them into the queue, and, mark them as visited by removing its entry from words set.
- For finding adjacent strings, replace every character at every index of a current string with a new character and check its entry in the words set(intermediate words).
- Whenever we’ll find endWord, return the level of the endWord since BFS always yields the shortest path.
Code
Word Ladder Leetcode Solution C++:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
queue<pair<string,int>> q;
q.push({beginWord,1});
unordered_set<string> words(wordList.begin(),wordList.end());
words.erase(beginWord);
while(!q.empty()){
string curr = q.front().first;
int level = q.front().second;
q.pop();
if(curr==endWord){
return level;
}
for(int i=0;i<(int)curr.length();i++){
string str = curr;
for(char ch='a';ch<='z';ch++){
str[i] = ch;
if(words.count(str)){
q.push({str,level+1});
words.erase(str);
}
}
}
}
return 0;
}
};Word Ladder Leetcode Solution Java:
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
Queue<String> q = new LinkedList<>();
q.offer(beginWord);
int level = 1;
Set<String> words = new HashSet<String>();
for(String word:wordList){
words.add(word);
}
words.remove(beginWord);
while(!q.isEmpty()){
int sz = q.size();
for(int k=0;k<sz;k++){
String curr = q.poll();
if(curr.equals(endWord)){
return level;
}
for(int i=0;i<curr.length();i++){
for(char ch='a';ch<='z';ch++){
String str = curr.substring(0,i) + ch + curr.substring(i+1);
if(words.remove(str)){
q.offer(str);
}
}
}
}
level++;
}
return 0;
}
}
Complexity Analysis for Word Ladder Leetcode Solution
Time Complexity
The time complexity of the above code is O(n*m^2) since the queue operates each word in the worst case(there are n-words), and for each word has max length as m, so a total number of iterations is n*m. Also, for each character of the string, we are making a copy of the current string which takes O(m) time again. Hence, the overall complexity of the solution is O(n*m^2) [Considering a good hash performs the search/deletion operation in O(1)].
Space Complexity
The space complexity of the above code is O(n*m^2) since we have total n-words and for each is of max length as m. Also, for each word, we’re forming the intermediate word which takes O(m) space.