Table of Contents
Problem Statement
Minimum Jumps to Reach Home LeetCode Solution says – A certain bug’s home is on the x-axis at position x.
Help them get there from position 0.
The bug jumps according to the following rules:
- It can jump exactly a positions forward (to the right).
- It can jump exactly b positions backward (to the left).
- It cannot jump backward twice in a row.
- It cannot jump to any forbidden positions.
The bug may jump forward beyond its home, but it cannot jump to positions numbered with negative integers.
Given an array of integers forbidden, where forbidden[i] means that the bug cannot jump to the position forbidden[i], and integers a, b, and x, return the minimum number of jumps needed for the bug to reach its home. If there is no possible sequence of jumps that lands the bug on position x, return -1.
Example:
Test Case 1:
Input:
forbidden = [6, 14, 17]
a = 3
b = 1
x = 13
Output:
7
Explanation:
i) For the first test case, there are various options to move from 0 to 13. But we can move from 0->3, 3->2, 2->5, 5->8, 8->7, 7->10, 10->13. It takes 7 steps. It is the minimum path we can take. So the answer is 7.
Approach
Idea:
Here on the first look, we might think that it is an Overlapping sub-problem. But the issue is here we are also moving backward. So we might fall into an infinite loop. So we can think of it as a graph having Back edges where we need to move from a source to the destination with constraints such as we can’t take Back edges twice in a row and we can’t go to certain positions which can be thought of as isolated vertex. If there is no way we can reach the destination starting from the source we need to return -1. 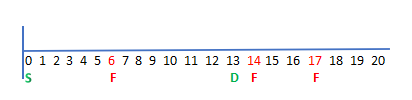
Position Tracking:

Code
Java Program for Minimum Jumps to Reach Home LeetCode Solution
class Solution {
public int minimumJumps(int[] forbidden, int a, int b, int x) {
int stepCount = 0, furthest = x + a + b;
Queue<Pair<Integer, Integer>> queue = new LinkedList();
queue.offer(new Pair(0, 0));
Set<Pair<Integer, Integer>> visited = new HashSet<>(queue);
for (int pos : forbidden) {
visited.add(new Pair(0, pos));
visited.add(new Pair(1, pos));
furthest = Math.max(furthest, pos + a + b);
}
while (!queue.isEmpty()) {
for (int size = queue.size(); size > 0; --size) {
Pair<Integer, Integer> p = queue.poll();
int dir = p.getKey(), pos = p.getValue();
if (pos == x) {
return stepCount;
}
Pair<Integer, Integer> forward = new Pair<>(0, pos + a), backward = new Pair<>(1, pos - b);
if (pos + a <= furthest && visited.add(forward)) {
queue.offer(forward);
}
if (dir == 0 && pos - b >= 0 && visited.add(backward)) {
queue.offer(backward);
}
}
++stepCount;
}
return -1;
}
}C++ Program for Minimum Jumps to Reach Home LeetCode Solution
class Solution {
public:
int minimumJumps(vector<int>& forbidden, int a, int b, int x) {
unordered_map<int,int> visited;
queue<pair<int,int>> positionQueue;
for(auto i:forbidden){
visited[i]=true;
}
positionQueue.push({0,0}) ;
int stepCount = 0;
while(!positionQueue.empty()){
int size = positionQueue.size() ;
while(size--){
auto curr = positionQueue.front() ;
positionQueue.pop() ;
int num = curr.first;
if(num == x){
return stepCount;
}
if(visited[num] == true){
continue;
}
visited[num]=true;
if(curr.second == 0 && num-b>=0) {
positionQueue.push({(num-b),1});
}
if(num <= 2000+b){
positionQueue.push({(num+a),0});
}
}
stepCount++;
}
return -1;
}
};Complexity Analysis for Minimum Jumps to Reach Home in Array LeetCode Solution
Time Complexity
The bug at most needs to reach furthest = max(x, forbidden) + a +b in order to arrive at x. So the time complexity is O(max(x, max(forbidden)) + a + b).
Space Complexity
Here for each possible position, we need to store the position. So the space complexity is O(max(x, max(forbidden)) + a + b).
Reference: https://en.wikipedia.org/wiki/Overlapping_subproblems