Table of Contents
Problem Statement
Brightest Position on Street LeetCode Solution – We are asked to assume a number line representing a street. This street contains lamp(s) on it. We are given a 2D integer array “lights”. Each lights[i] = [position_i, range_i] indicates that there is a street lamp on position_i which can brighten the street from [position_i – range_i, position_i + range_i] (both inclusive). The brightness of a position p is defined as the number of street lamps that lit the position p. We need to return to the brightest position on the street. In case there are multiple brightest positions, the lowest one is the answer.
Examples & Explanation
Example 1:
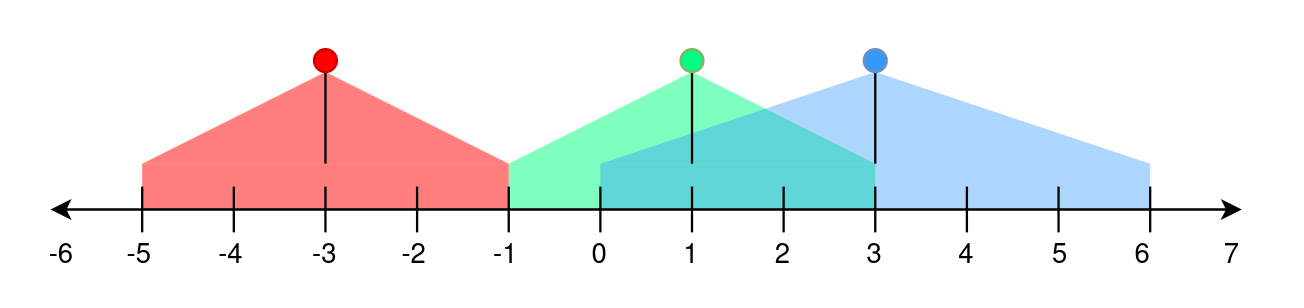
Input: lights = [[-3,2],[1,2],[3,3]] Output: -1 Explanation: The first street lamp lights up the area from [(-3) - 2, (-3) + 2] = [-5, -1]. The second street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3]. The third street lamp lights up the area from [3 - 3, 3 + 3] = [0, 6]. Position -1 has a brightness of 2, illuminated by the first and second street light. Positions 0, 1, 2, and 3 have a brightness of 2, illuminated by the second and third street light. Out of all these positions, -1 is the smallest, so return it.
Example 2:
Input: lights = [[1,0],[0,1]] Output: 1 Explanation: The first street lamp lights up the area from [1 - 0, 1 + 0] = [1, 1]. The second street lamp lights up the area from [0 - 1, 0 + 1] = [-1, 1]. Position 1 has a brightness of 2, illuminated by the first and second street light. Return 1 because it is the brightest position on the street.
Example 3:
Input: lights = [[1,2]] Output: -1 Explanation: The first street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3]. Positions -1, 0, 1, 2, and 3 have a brightness of 1, illuminated by the first street light. Out of all these positions, -1 is the smallest, so return it.
Approach
This problem can be easily solved using an array or a map. For every point that is lit by a lamp, we will add one to it. Start traversing from the lowest point and store the position of the max brightest point in the array. We can use this approach to solve this problem for small position values. According to the constraints, position[i] varies from -10^8 to 10^8. This solution will cause TLE. Can we do better?
If we observe, we actually don’t need to keep a track of all the values lit by a particular lamp since we need to return only the smallest position. So, instead of adding 1 to all the positions lit by lamp, we only increment the lowest point, i.e. map[poisiton[i]-range[i]]++ and decrement the value of map[position[i] + range[i] + 1]. We can then simply traverse from the lowest position and keep incrementing a count variable to keep a track of the max bright point. Whenever a point is not light up, the value of the count will decrement.
Code
C++ code for Brightest Position on Street
class Solution {
public:
int brightestPosition(vector<vector<int>>& lights) {
map<int,int> brightness;
for(auto& light: lights) {
brightness[light[0]-light[1]]++, brightness[light[0]+light[1]+1]--;
}
int maxBrightness=0, maxBrightPoint=0, cntBright=0;
for(auto& bright: brightness){
cntBright+=bright.second;
if(cntBright > maxBrightness) {
maxBrightness = cntBright;
maxBrightPoint = bright.first;
}
}
return maxBrightPoint;
}
};Java code for Brightest Position on Street
class Solution {
public int brightestPosition(int[][] lights) {
int length = lights.length;
int left = 0, right = 0;
TreeMap<Integer, Integer> treemap = new TreeMap<>();
for(int[] light : lights) {
left = (light[0] - light[1]);
right = (light[0] + light[1] + 1);
treemap.put(left, (treemap.getOrDefault(left, 0) + 1));
treemap.put(right, (treemap.getOrDefault(right, 0) - 1));
}
int countBright = 0, maxBrightness = 0, maxBrightPoint = 0;
for(Map.Entry<Integer, Integer> entry : treemap.entrySet()) {
countBright += entry.getValue();
if(maxBrightness < countBright) {
maxBrightness = countBright;
maxBrightPoint = entry.getKey();
}
}
return maxBrightPoint;
}
}Complexity Analysis for Brightest Position on Street LeetCode Solution
- Time complexity: O(N*logN), N=length of given 2D array
- We are traversing the 2D array to create a map, for each lights[i], we add or update 2 values in the map, sorting of the map takes O(logN)
- maximum values in the map could be 2*n
- another loop traverses on all values in the sorted map, total time = O(2*N*logN) which is equivalent to O(N*logN)
- Space complexity: O(N)
- An additional Map is required to keep a track of bright points