Table of Contents
Problem Statement
Closest Leaf in a Binary Tree LeetCode Solution – Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.
Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.
Example
Test Case 1:
Input:
root = [1, 3, 2]
k = 1
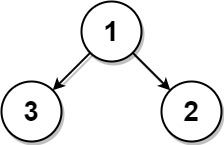
Output:
2
Explanation
Either 2 or 3 is the nearest leaf node to the target of 1.
Approach:
The required leaf will be either the descendant leaf of the given node (distance from a given node to leaf) or the descendant leaf of the ancestor of the given node (distance from given node to ancestor + distance from ancestor node to leaf)
Traverse all the nodes in the tree in the helper function, as soon as we find the given node, call another function(func) until we find the leaf, as we find the leaf update its distance from the given node in a map called direct.
when we find the given node then stop going further in the helper function return positive value (1), to let know the ancestor that it is the ancestor of the given node. And as we go (returning) to its previous ancestors we also return the distance of the given node to its ancestor.
Then if the return value is positive in the helper function (we found an ancestor of the given node), call func function and calculate the distance to its leaf, as soon as we find a leaf, update the distance which is (distance from the given node to ancestor + distance from ancestor to leaf node) and add this other map indirect.
At last traverse both maps (direct and indirect) and find the answer. “direct” map contains the distance to the descendant leaf of given nodes. “indirect” map contains the distance from the given node to the ancestor node + the distance of the ancestor node to its leaf node.
flag parameter in func function is used to differentiate between these two cases.
Code for Closest Leaf in a Binary Tree
Java Program
class Solution {
int ans = Integer.MAX_VALUE;
int res = -1;
int check = 1;
Map<Integer,Integer> direct, indirect;
public int findClosestLeaf(TreeNode root, int k) {
if(root == null)
return 0;
direct = new HashMap<>();
indirect = new HashMap<>();
func(root,k);
getRes(true);
getRes(false);
return res;
}
public int func(TreeNode root,int k){
int val = root.val,left = -1, right = -1;
if(val == k){
helper(root,0,true,k);
return 1;
}else{
if(root.left != null){
left = func(root.left,k);
}
if(root.right != null){
right = func(root.right,k);
}
if(left > 0 || right > 0){
int t = left > right ? left : right;
helper(root,t,false,k);
return t + 1;
}
return 0;
}
}
public void helper(TreeNode root,int dist,boolean flag,int k){
int val = root.val;
if(!flag){
if(val == k)
return;
if(indirect.containsKey(val))
return;
}
if(root.left == null && root.right == null){
if(flag){
direct.put(val,dist);
}else{
indirect.put(val,dist);
}
return;
}
if(root.left != null){
helper(root.left,dist+1,flag,k);
}
if(root.right != null){
helper(root.right,dist+1,flag,k);
}
}
public void getRes(boolean flag){
Map<Integer,Integer> map = (flag) ? direct : indirect;
for(int key:map.keySet()){
int val = map.get(key);
if(val < ans){
ans = val;
res = key;
}
}
}
}C++ Program
class Solution {
private:
// updated:
// 1. at the node with value k, so that it is the shortest path to a leaf in its subtree
// 2. at any ancester of k, so that it is the shortest path to a leaf going through the ancester node
int result;
int dis = 1000;
// returns {dis_to_leaf, leaf_val} if root is not an ancester of k
// return {dis_to_target, k} if root is k or an ancester of k
pair<int, int> helper(TreeNode* root, int k) {
// base case: if root is a leaf, return {0, val}
if (root->left == nullptr && root->right == nullptr) {
if (root->val == k) {
result = root->val;
dis = 0;
}
return {0, root->val};
}
// var to store left and right sub tree result
pair<int, int> l = {1000, -1};
pair<int, int> r = {1000, -1};
if (root->left != nullptr) {
l = helper(root->left, k);
}
if (root->right != nullptr) {
r = helper(root->right, k);
}
int curr_dis = min(l.first, r.first) +1;
int curr_res;
if (curr_dis-1 == l.first) {
curr_res = l.second;
} else {
curr_res = r.second;
}
// attempt to update the result if root->val == k
if (root->val == k) {
dis = min(dis, curr_dis);
if (dis == curr_dis) {
result = curr_res;
}
return {0, k};
}
// attempt to update the result if root is an ancester of k
if (l.second == k || r.second == k) {
int dis_from_k = l.second == k?l.first:r.first;
int dis_from_leaf = l.second == k?r.first:l.first;
int leaf = l.second == k?r.second:l.second;
dis = min(dis, dis_from_leaf + dis_from_k + 2);
if (dis == dis_from_leaf + dis_from_k+2) {
result = leaf;
}
return {dis_from_k+1, k};
}
// pass on value if cannot update result
return {curr_dis, curr_res};
}
public:
int findClosestLeaf(TreeNode* root, int k) {
if (root == nullptr) {
return -1;
}
pair<int, int> root_res = helper(root, k);
if (root_res.second!= k && root_res.first < dis) {
return root_res.second;
} else {
return result;
}
}
};Complexity Analysis for Closest Leaf in a Binary Tree LeetCode Solution
Time Complexity will be
- Getting the node in contention – O(h)
- Building the parent-child map – O(n)
- BFS – O(n)
Overall time complexity – O(n)
Space Complexity will be
- Getting the node in contention – O(h), call stack
- Parent-child map – O(n)
- The queue for BFS – O(n)
Overall space complexity – O(n)
Reference: https://en.wikipedia.org/wiki/Breadth-first_search