Diagonal Traversal LeetCode Solution

Difficulty Level Medium
Frequently asked in Amazon Apple DoorDash Facebook Google Microsoft Robinhood Visa
Goldmann SachsViews 3968

Problem Statement

Diagonal Traversal LeetCode Solution – Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Diagonal Traversal LeetCode Solution

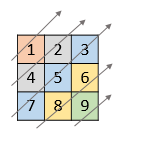
Explanation for Diagonal Traversal LeetCode Solution

Key Idea

The first row and the last column in this problem would serve as the starting point for the corresponding diagonal. Given an element inside a diagonal, say [i, j], we can either go up the diagonal by going one row up and one column ahead i.e. [i – 1, j + 1] or, we can go down the diagonal by going one row down and one column to the left i.e. [i + 1, j – 1]. Note that this applies to diagonals that go from right to left only. The math would change for the ones that go from left to right.

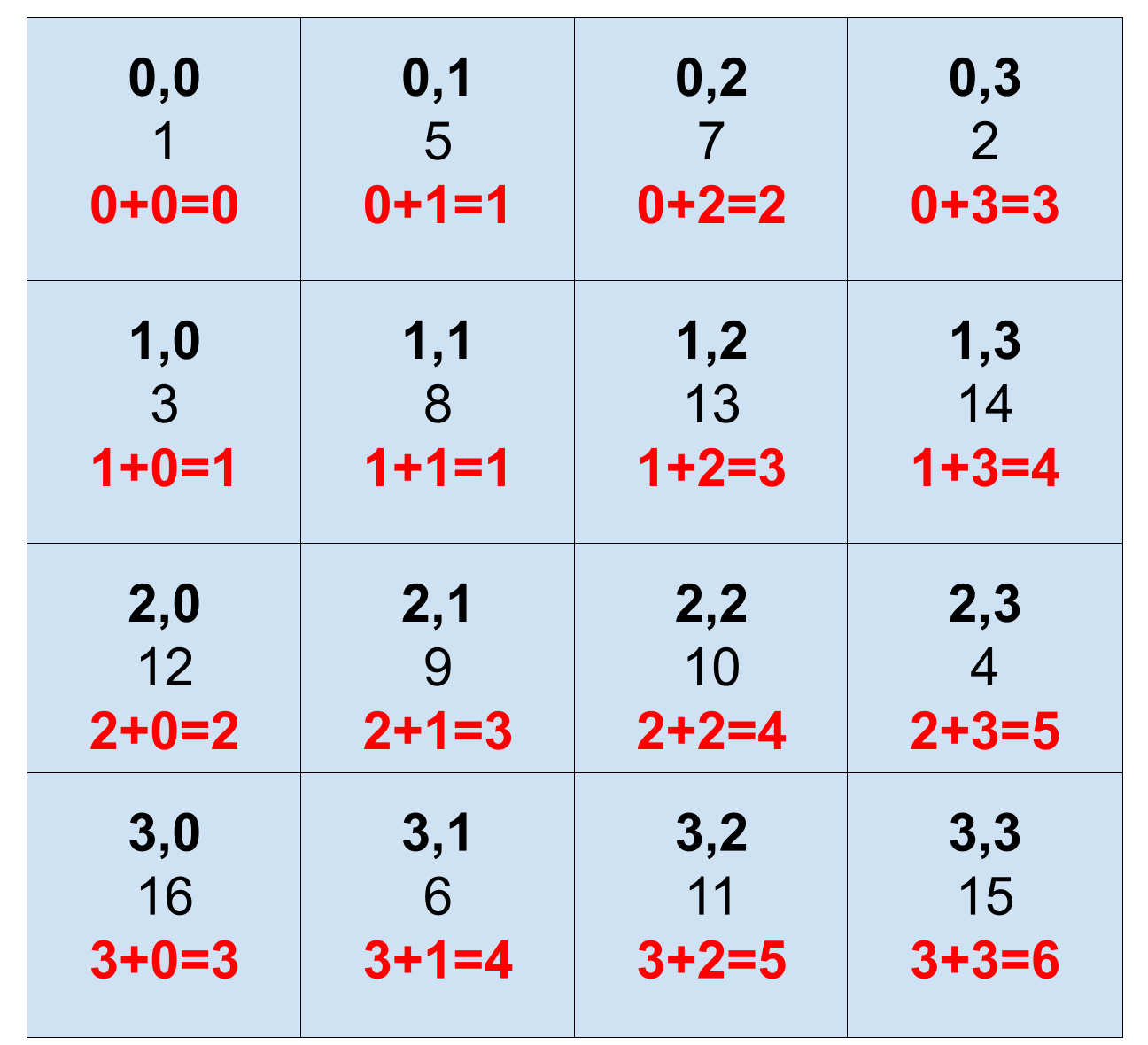
In a 2D matrix, elements in the same diagonal have the same sum of their indices.

So if we have all elements with the same sum of their indices together, then it’s just a matter of printing those elements in order.

Algorithm

  1. Insert all elements into an appropriate bucket i.e. nums[i][j] in (i+j)th bucket.
  2. For each bucket starting from 0 to max, print all elements in the bucket.
    Note: Here, diagonals are from bottom to top, but we traversed the input matrix from the first row to the last row. Hence we need to print the elements in reverse order.

Diagonal Traversal LeetCode Solution

Code

C++ Code for Diagonal Traversal

class Solution {
public:
   vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
        if(matrix.empty()) return {};
        
        const int N = matrix.size();
        const int M = matrix[0].size();
        
        vector<int> res;
        for(int s = 0; s <= N + M - 2; ++s)
        {
            // for all i + j = s
            for(int x = 0; x <= s; ++x) 
            {
                int i = x;
                int j = s - i;
                if(s % 2 == 0) swap(i, j);

                if(i >= N || j >= M) continue;
                
                res.push_back(matrix[i][j]);
            }
        }
        
        return res;
    }
};

Java Code for Diagonal Traversal

class Solution {
   public int[] findDiagonalOrder(int[][] matrix) {
        if (matrix.length == 0) return new int[0];
        int r = 0, c = 0, m = matrix.length, n = matrix[0].length, arr[] = new int[m * n];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = matrix[r][c];
            if ((r + c) % 2 == 0) { // moving up
                if      (c == n - 1) { r++; }
                else if (r == 0)     { c++; }
                else            { r--; c++; }
            } else {                // moving down
                if      (r == m - 1) { c++; }
                else if (c == 0)     { r++; }
                else            { r++; c--; }
            }   
        }   
        return arr;
    }
}

Python Code for Diagonal Traversal

class Solution:
    def findDiagonalOrder(self, matrix):
        entries = [(i+j, (j, i)[(i^j)&1], val)
                   for i, row in enumerate(matrix)
                   for j, val in enumerate(row)]
        return [e[2] for e in sorted(entries)]

Complexity Analysis for Diagonal Traversal LeetCode Solution

Time Complexity

O(n^2) since a complete matrix traversal is required.

Space Complexity

O(n) since we use a hashmap to store the sum of row + col keys.

Reference: https://docs.oracle.com/javase/8/docs/api/java/util/HashMap.html

Translate »