Diagonal Traverse LeetCode Solution

Table of Contents

Problem Statement

Diagonal Traverse LeetCode Solution – Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

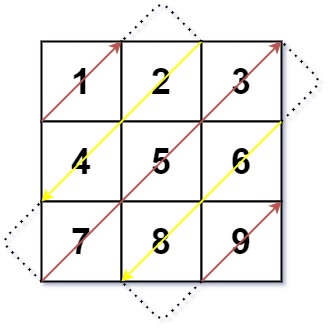
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Explanation

Consider the indices of the diagonals of an NxM matrix. Let’s use a 4×4 matrix as an example:

(0, 0) (0, 1) (0, 2) (0, 3)

(1, 0) (1, 1) (1, 2) (1, 3)

(2, 0) (2, 1) (2, 2) (2, 3)

(3, 0) (3, 1) (3, 2) (3, 3)

The first diagonal is (0, 0). The second is (0, 1), (1, 0), the third is (2, 0), (1, 1), (0, 2), etc.

It should be clear that the sum of row i and column j is equal to the index of the diagonal (diagonal number – 1). e.g. for the second diagonal (index 1), all possible pairings of (i, j) sum to 1, i.e. i + j = 1 for the 2nd diagonal. The maximum diagonal index is simply ((N-1) + (M-1)) = N + M - 2

So to solve the problem we simply need to iterate through all possible diagonal indices (denote this as s) and find all possible pairs (i, j) such that i + j = s. The only thing we need to concern ourselves about is the order. We can find the ordering by looking at whether the diagonal index is even or odd. When the diagonal index is even we want to the first pair to be (s, 0) and when it is odd when wanting the first pair to be (0, s), and we decrease or increase i/j by 1 accordingly.

Code

C++ Code for Diagonal Traversal

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
        if(matrix.empty()) return {};
        
        const int N = matrix.size();
        const int M = matrix[0].size();
        
        vector<int> res;
        for(int s = 0; s <= N + M - 2; ++s)
        {
            // for all i + j = s
            for(int x = 0; x <= s; ++x) 
            {
                int i = x;
                int j = s - i;
                if(s % 2 == 0) swap(i, j);

                if(i >= N || j >= M) continue;
                
                res.push_back(matrix[i][j]);
            }
        }
        
        return res;
    }
};

Java Code for Diagonal Traversal

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        HashMap<Integer,List<Integer>> map=new HashMap<>();
        for (int i=0;i<mat.length;i++) {
            for(int j=0;j<mat[i].length;j++) {
                int key=i+j;
                if(map.containsKey(key)) map.get(key).add(mat[i][j]);
                else {
                    map.put(key,new ArrayList<Integer>());
                    map.get(key).add(mat[i][j]);
                     }
            }
        }
        int curr=0;
        int index=0;
        boolean check=false;
        int[] ans=new int[mat.length*mat[0].length];
        while (true) {
            if(!map.containsKey(curr)) break;
            List<Integer> a=map.get(curr);
            if(check) {
                for(int i=0;i<a.size();i++) {
                    ans[index++]=a.get(i);
                }
                check=!check;
            }
            else {
                for(int i=a.size()-1;i>=0;i--) {
                    ans[index++]=a.get(i);
                }
                check=!check;
            }
            curr++;
        }
        return ans;
    }
}

Python Code for Diagonal Traversal

class Solution(object):
    def findDiagonalOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        result = [ ]
        dd = collections.defaultdict(list)
        if not matrix: return result
        # Step 1: Numbers are grouped by the diagonals.
        # Numbers in same diagonal have same value of row+col
        for i in range(0, len(matrix)):
            for j in range(0, len(matrix[0])):
                dd[i+j+1].append(matrix[i][j]) # starting indices from 1, hence i+j+1.
        # Step 2: Place diagonals in the result list.
        # But remember to reverse numbers in odd diagonals.
        for k in sorted(dd.keys()):
            if k%2==1: dd[k].reverse()
            result += dd[k]
        return result