Find Median from Data Stream LeetCode Solution

Difficulty Level Hard
Frequently asked in Adobe Airbnb Amazon Apple Bloomberg ByteDance Citadel DoorDash eBay Expedia Facebook Goldman Sachs Google Indeed IXL LinkedIn Microsoft Nvidia Oracle Paytm Salesforce SAP Snapchat Spotify Twilio Twitter Uber VMware Wish
Walmart Global techViews 3258

Problem Statement

Find Median from Data Stream LeetCode Solution – The median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value and the median is the mean of the two middle values.

  • For example, for arr = [2,3,4], the median is 3.
  • For example, for arr = [2,3], the median is (2 + 3) / 2 = 2.5.

Implement the MedianFinder class:

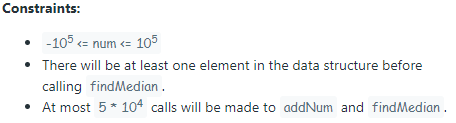
  • MedianFinder() initializes the MedianFinder object.
  • void addNum(int num) adds the integer num from the data stream to the data structure.
  • double findMedian() returns the median of all elements so far. Answers within 10-5 of the actual answer will be accepted.

Find Median from Data Stream LeetCode Solution

Example

Test Case 1:

Input:

[“MedianFinder”, “addNum”, “addNum”, “findMedian”, “addNum”, “findMedian”]

[[], [1], [2], [], [3], []]

Output:

[null, null, null, 1.5, null, 2.0]

Explanation:

MedianFinder medianFinder = new MedianFinder();

medianFinder.addNum(1); // arr = [1]

medianFinder.addNum(2); // arr = [1, 2]

medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)

medianFinder.addNum(3); // arr[1, 2, 3]

medianFinder.findMedian(); // return 2.0

Approach:

The invariant of the algorithm is two heaps, small and large, each representing half of the current list. The length of the smaller half is kept to be n / 2 at all times and the length of the larger half is either n / 2 or n / 2 + 1 depending on n’s parity.

This way we only need to peek at the two heaps of top numbers to calculate the median.

Any time before we add a new number, there are two scenarios, (total n numbers, k = n / 2):

(<span class="hljs-number">1</span>) <span class="hljs-function">length <span class="hljs-title">of</span> <span class="hljs-params">(small, large)</span> </span>== (k, k)
(<span class="hljs-number">2</span>) <span class="hljs-function">length <span class="hljs-title">of</span> <span class="hljs-params">(small, large)</span> </span>== (k, k + <span class="hljs-number">1</span>)

After adding the number, total (n + 1) numbers, they will become:

(<span class="hljs-number">1</span>) <span class="hljs-function">length <span class="hljs-title">of</span> <span class="hljs-params">(small, large)</span> </span>== (k, k + <span class="hljs-number">1</span>)
(<span class="hljs-number">2</span>) <span class="hljs-function">length <span class="hljs-title">of</span> <span class="hljs-params">(small, large)</span> </span>== (k + <span class="hljs-number">1</span>, k + <span class="hljs-number">1</span>)

Here we take the first scenario, for example, we know the large will gain one more item and the small will remain the same size, but we cannot just push the item into large. What we should do is push the new number into small and pop the maximum item from small then push it into large (all the pop and push here are heappop and heappush). By doing this kind of operation for the two scenarios we can keep our invariant.

Therefore to add a number, we have 3 O(log n) heap operations. Luckily the heapq provided us a function “heappushpop” which saves some time by combining two into one. The document says:

Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop().

Altogether, the add operation is O(logn), and The find median operation is O(1).

Note that the heapq in python is a min-heap, thus we need to invert the values in the smaller half to mimic a “max heap”.

Code for Find Median from Data Stream

Java Program

class MedianFinder {

    private PriorityQueue<Integer> small = new PriorityQueue<>(Collections.reverseOrder());
    private PriorityQueue<Integer> large = new PriorityQueue<>();
    private boolean even = true;

    public double findMedian() {
        if (even)
            return (small.peek() + large.peek()) / 2.0;
        else
            return small.peek();
    }

    public void addNum(int num) {
        if (even) {
            large.offer(num);
            small.offer(large.poll());
        } else {
            small.offer(num);
            large.offer(small.poll());
        }
        even = !even;
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

Python Program

from heapq import *


class MedianFinder:
    def __init__(self):
        self.small = []  # the smaller half of the list, max heap (invert min-heap)
        self.large = []  # the larger half of the list, min heap

    def addNum(self, num):
        if len(self.small) == len(self.large):
            heappush(self.large, -heappushpop(self.small, -num))
        else:
            heappush(self.small, -heappushpop(self.large, num))

    def findMedian(self):
        if len(self.small) == len(self.large):
            return float(self.large[0] - self.small[0]) / 2.0
        else:
            return float(self.large[0])

Complexity Analysis for Find Median from Data Stream LeetCode Solution

Time Complexity: O(logn), as at worst, there are three heap insertions and two heap deletions from the top. Each of these takes about O(\log n) time..

Space Complexity: O(n), as we are using linear space to hold input in containers..

Translate »