Time Based Key-Value Store LeetCode Solution

Problem Statement

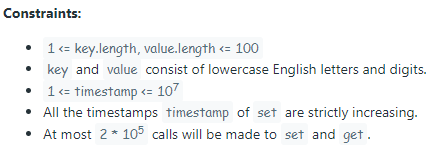
Time Based Key-Value Store LeetCode Solution – Design a time-based key-value data structure that can store multiple values for the same key at different time stamps and retrieve the key’s value at a certain timestamp.

Implement the TimeMap class:

• TimeMap() Initializes the object of the data structure.
• void set(String key, String value, int timestamp) Stores the key key with the value value at the given time timestamp.
• String get(String key, int timestamp) Returns a value such that set was called previously, with timestamp_prev <= timestamp. If there are multiple such values, it returns the value associated with the largest timestamp_prev. If there are no values, it returns "".

Example

Test Case 1:

Input:

[“TimeMap”, “set”, “get”, “get”, “set”, “get”, “get”] [[], [“foo”, “bar”, 1], [“foo”, 1], [“foo”, 3], [“foo”, “bar2”, 4], [“foo”, 4], [“foo”, 5]]

Output:

[null, null, “bar”, “bar”, null, “bar2”, “bar2”]

Explanation:

TimeMap timeMap = new TimeMap();

timeMap.set(“foo”, “bar”, 1); // store the key “foo” and value “bar” along with timestamp = 1.

timeMap.get(“foo”, 1); // return “bar”

timeMap.get(“foo”, 3); // return “bar”, since there is no value corresponding to foo at timestamp 3 and timestamp 2, then the only value is at timestamp 1 is “bar”.

timeMap.set(“foo”, “bar2”, 4); // store the key “foo” and value “bar2” along with timestamp = 4.

timeMap.get(“foo”, 4); // return “bar2”

timeMap.get(“foo”, 5); // return “bar2”

Approach:

We can use a HashMap to store all occurrences of a key. Note that since calls to the set method are strictly increasing, we can just add occurrences to a List, which will by default be in sorted order, allowing us to leverage binary search when looking for the valid occurrence of a key (ArrayList for O(1) lookup time).

Before performing binary search I added a couple of explicit edge case checks, if the timestamp we’re checking is less than the minimum has seen timestamp (so, the first element in the list), there’s no valid value. If the timestamp we’re checking is greater than the maximum seen timestamp (so, the last element in the list), just return the value at the max seen timestamp.

We will use .upper_bound() to find a value that is greater than the timestamp.
We will need to go one element back to get the correct value.
But before going 1 element back we need to check if the current iterator points at the very first element.

Code for Time Based Key-Value Store

C++ Program

class TimeMap {
public:
unordered_map<string, map<int, string>> keys;
public:
    TimeMap() {}
    
    void set(string key, string value, int timestamp) {
        keys[key][timestamp] = value;
    // inserting into unordered_map O(1)
    // inserting into map O(log n)
    // due to binary search on the tree.
    }
    
    string get(string key, int timestamp) {
        if (keys.count(key)) {
            auto& map = keys[key]; // taking from unordered_map O(1)
            auto it = map.upper_bound(timestamp); // taking from map O(log n)
                          // due to binary search on the tree.
            if (it == map.begin()) {
                return "";
            }
            return (--it)->second;
        }
        return "";
    }
};

/**
 * Your TimeMap object will be instantiated and called as such:
 * TimeMap* obj = new TimeMap();
 * obj->set(key,value,timestamp);
 * string param_2 = obj->get(key,timestamp);
 */

Java Program

class TimeMap {

    private Map<String,TreeMap<Integer,String>> map;

    /** Initialize your data structure here. */
    public TimeMap() {
        map = new HashMap<>();
    }

    public void set(String key, String value, int timestamp) {
        if(!map.containsKey(key)) {
            map.put(key,new TreeMap<>());
        }
        map.get(key).put(timestamp,value);
    }

    public String get(String key, int timestamp) {
        TreeMap<Integer,String> treeMap = map.get(key);
        if(treeMap==null) {
            return "";
        }
        Integer floor = treeMap.floorKey(timestamp);
        if(floor==null) {
            return "";
        }
        return treeMap.get(floor);
    }
}

/**
 * Your TimeMap object will be instantiated and called as such:
 * TimeMap obj = new TimeMap();
 * obj.set(key,value,timestamp);
 * String param_2 = obj.get(key,timestamp);
 */

Complexity Analysis for Time Based Key-Value Store LeetCode Solution

Assuming n is the number of set operations, and m is the number of get operations:

• Time Complexity:
  • Set: O(1) single operation, and total O(n).
    Note: assuming timestamps are only increasing. If not, it’s O(n log n).
  • Get: O(log n) for a single operation, and total O(m log n).
• Space Complexity: O(n) (assuming every { timestamp, value } is unique).