Koko Eating Bananas LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Airbnb Amazon Apple DoorDash Facebook GoogleViews 1958

Problem Statement

Koko Eating Bananas LeetCode Solution – Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.

Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.

Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.

Return the minimum integer k such that she can eat all the bananas within h hours.

 

Example

Test Case 1:

Input:

piles = [3, 6, 7, 11]

h = 8

Output:

4

Approach:

Let’s understand the solution, as we are going to be using Binary Search we have given an Array [3,6,7,11] And we have to eat every single pile of bananas in less than or equal to hours = 8. If we are not able to do that Guard will kill KOKO [just a joke]

As we know that the potential rate that we’re eating bananas at k is going to be between 1 that’s the minimum it could possibly be. The max it could possibly be is going to be whatever the max in our input array is and that is 11. So, then we’re going to initialize a range like this k = [1,2,3,4,5,6,7,8,9,10,11] the entire range we have. Going all the way from 1 to the max value 11.

Koko Eating Bananas LeetCode Solution

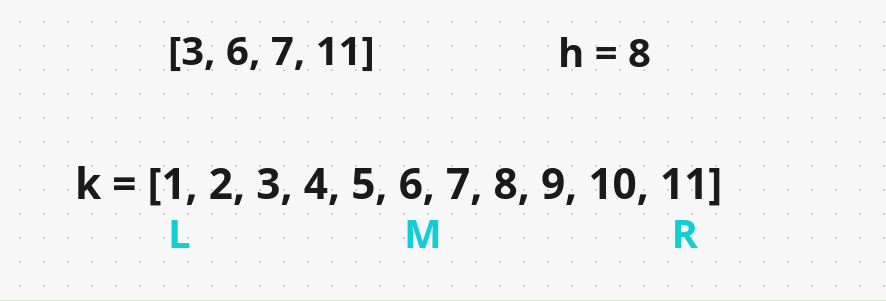
So, in other words, we’re going to have a left pointer at the minimum and a right pointer at the maximum. Then we compute the middle by taking the average of left & right / 2 i.e. 1 + 11 / 2 = 6. So, our middle will be here at 6 in other words that k we’re trying is going to be here at this rate that we’re going to eat bananas at the rate of 6.

Now let’s check can we eat all the piles of bananas at the rate of 6. Let’s check it.

Koko Eating Bananas LeetCode Solution

If you see that we just eat all piles of bananas in 6 hours is that a good value. Well, it is less than or equal to 8 hours, but still, we have to find the minimum possible k value. This might be the solution but less try is there any smaller k value than 6.
So, we decrement our right pointer to mid – 1 because there might be the best possible solution available.

So, once again we compute the middle by taking the average of left & right / 2 i.e. 1 + 5 / 2 = 3 our k is here at 3 value

Now let’s check can we eat all the piles of bananas at the rate of 3. Let’s check it.

Koko Eating Bananas LeetCode Solution

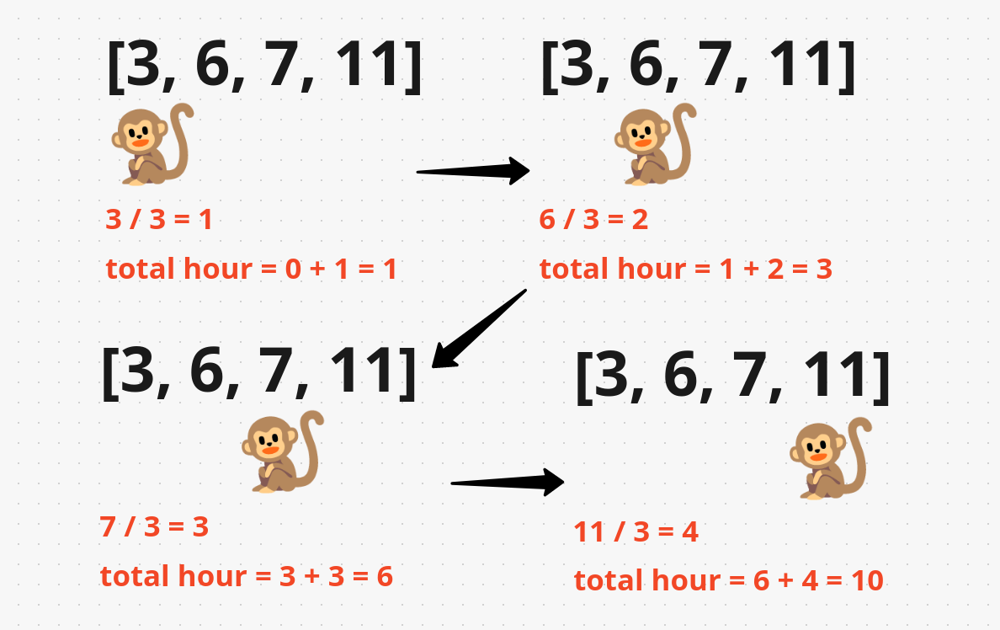
If you see that we just eat all piles of bananas in 10 hours but if you see we went over 8 hours we took too long to eat all the bananas. So, eating at a rate of 3 didn’t work.
Let’s start searching to the right of our range we increment our left pointer to mid + 1 but remember when we shift our right pointer from the last position to mid -1 we just consider that this range will not work. And that’s how Binary search work!

So, once again we compute the middle by taking the average of left & right / 2 i.e. 4 + 5 / 2 = 4 our k is here at the 4 value

Now let’s check can we eat all the piles of bananas at the rate of 4. Let’s check it.

Koko Eating Bananas LeetCode Solution

If you see that we just eat all piles of bananas in 8 hours. So, we were able to eat all bananas in less than or equal to 8 hours if we had a rate of 4. Let’s compare this with our current result. So, far we find a value of 6 we update this 6 and we can say there is a smaller rate we can use i.e. 4.

Code for Koko Eating Bananas

Java Program

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left = 1;
        int right = 1000000000;
        
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(canEatInTime(piles, mid, h)) right = mid - 1;
            else left = mid + 1;
        }
        return left;
    }
    public boolean canEatInTime(int piles[], int k, int h){
        int hours = 0;
        for(int pile : piles){
            int div = pile / k;
            hours += div;
            if(pile % k != 0) hours++;
        }
        return hours <= h;
    }
}

C++ Program

class Solution {
public:
    int minEatingSpeed(vector<int>& piles, int h) {
        int left = 1;
        int right = 1000000000;
        
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(canEatInTime(piles, mid, h)) right = mid - 1;
            else left = mid + 1;
        }
        return left;
    }
    bool canEatInTime(vector<int>& piles, int k, int h){
        int hours = 0;
        for(int pile : piles){
            int div = pile / k;
            hours += div;
            if(pile % k != 0) hours++;
        }
        return hours <= h;
    }
};

Complexity Analysis for Koko Eating Bananas LeetCode Solution

Time Complexity:- O(N * log(M)) where N is no of piles & M is the range of K (left to right)

Space Complexity:- O(1) as not using any extra space

Translate »