Number of Closed Islands Leetcode Solution

Difficulty Level Medium
Frequently asked in Amazon Apple Bloomberg Coupang Facebook Google Microsoft Oracle UberViews 3428

Problem Statement :

Number of Closed Islands Leetcode Solution – Given a 2D grid consisting of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example :

Example 1 

Number of Closed Islands Leetcode Solution

Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are surrounded by water (group of 1s).

 

Example 2

 

Number of Closed Islands Leetcode Solution

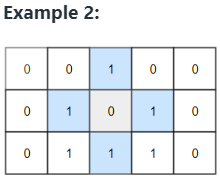
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Constraints :

Number of Closed Islands Leetcode Solution

Approach :

Idea

  • Now, pay attention to the edges, if we look, we find that the land  (0’s)  at the edges can never be part of a closed island, by the definition of a closed island, the land ( 0’s )  must be closed by water ( 1’s ) In all four directions.

  • Edges of the grid are first row (r = 0), Last row (r = n-1), First Column (c = 0), Last column (c = m-1).

Algorithm :

  • Traverse the grid and check if the edges of the grid are zero.
  • If the grid[i][j] in the edges is zero then do a DFS traversal and mark them as water, as land on the edges cannot be closed islands.
  • Through DFS traversal on the edges, all components attached to that edge will become water.
  • After the traversal of the grid, do a traversal again and call DFS for the remaining land (0’s).
  • The second traversal will work the same as the number of islands and returns valid closed islands.

Code for Number of Closed Islands Leetcode Solution

Java  Code

class Solution {
    int DIR[][]={{0,1},{1,0},{-1,0},{0,-1}};
    public int closedIsland(int[][] grid) {
        int n=grid.length;
        int m=grid[0].length;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(i==0 || j==0 ||i ==n-1 || j==m-1){
                    dfs(grid,i,j);
                }
            }
        }
            int ans=0;
             for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
               if(grid[i][j]==0){
                    dfs(grid,i,j);
                   ans++;
               }
            }
        }
            return ans;
    }
    
    public void dfs(int[][]grid,int r,int c){
        
         if(r<0||c<0||r>=grid.length||c>=grid[0].length||grid[r][c]==1)return ;
        grid[r][c]=1;
        
        for(int[]d:DIR){
            int nr= r+d[0];
            int nc=c+d[1];
           
            dfs(grid,nr,nc);
        }
    }
}

C++  Code

class Solution {
public:
    int DIR[4][2]={{0,1},{1,0},{-1,0},{0,-1}};
    int closedIsland(vector<vector<int>>& grid) {
        int n=grid.size();
        int m=grid[0].size();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(i==0 || j==0 ||i ==n-1 || j==m-1){
                    dfs(grid,i,j);
                }
            }
        }
            int ans=0;
             for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
               if(grid[i][j]==0){
                    dfs(grid,i,j);
                   ans++;
               }
            }
        }
            return ans;
    }
    
    void dfs(vector<vector<int>>& grid,int r,int c){
        
         if(r<0||c<0||r>=grid.size()||c>=grid[0].size()||grid[r][c]==1)return ;
        grid[r][c]=1;
        for(auto & d:DIR){
            int nr= r+d[0];
            int nc=c+d[1];
            dfs(grid,nr,nc);
        }
    }
};

Complexity Analysis for Number of Closed Islands Leetcode Solution

Time Complexity

The time complexity of the above code is O(n*m), as we are traversing each element of the grid always twice. Here n and m are the numbers of rows and number of columns respectively.

Space Complexity 

O(1), we have not utilized any extra space.

Translate »