Missing Element in Sorted Array LeetCode Solution

Table of Contents

Problem Statement:

Missing Element in Sorted Array LeetCode Solution – Given an integer array nums which are sorted in ascending order and all of its elements are unique and given also an integer k, return the kth missing number starting from the leftmost number of the array.

Example:

Example 1

Input: nums = [4,7,9,10], k = 3
Output: 8
Explanation: The missing numbers are [5,6,8,...], hence the third missing number is 8.

Example 2

Input: nums = [4,7,9,10], k = 1
Output: 5
Explanation: The first missing number is 5.

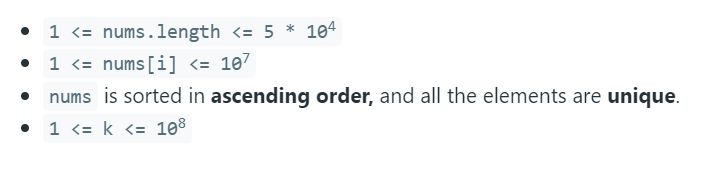
Constraint:

Explanation:

The elements of the array are unique and sorted in ascending order.
we need to return the kth missing number starting from the leftmost number of the array.
In the above example 1, the leftmost number is 4
A few missing numbers are:

1st missing number: 5

2nd missing number: 6

3rd missing number: 8

Note: 7 is present in nums so the next missing number after 6 is 8

In the given constraint nums[i] in between [1 to 10^7] and the nums of length in between [1 to 5*10^4].

Observation:

If we observe, we can see the array is sorted in ascending order and asking for the kth missing number. So, there is a high probability that we can use Binary Search in the question.

Approach:

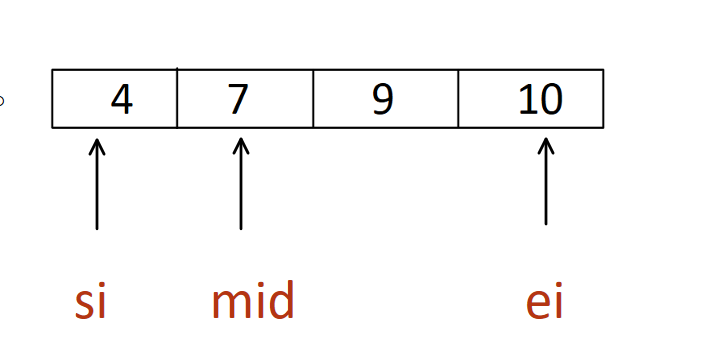
In Binary Search we use two pointers startIndex (si) and endIndex(ei) and find the midIndex (mid) [startIndex + (endIndex -startIdx)/2] then we will narrow our search area.

[ si=0, ei=3 mid= 0 + (3-0)/2 ]

How do we narrow our search area? Before answering this question, let us first discuss how we find out how many missing numbers are present in between nums[0] and nums[mid].

missing-Element-count = nums[mid] – (mid+nums[0]) = 7-(1+4) = 2

In between mid-index-Element [7] and leftmost-Element [4], only 5 and 6 are not present that is only two missing numbers but we want 3rd missing number.

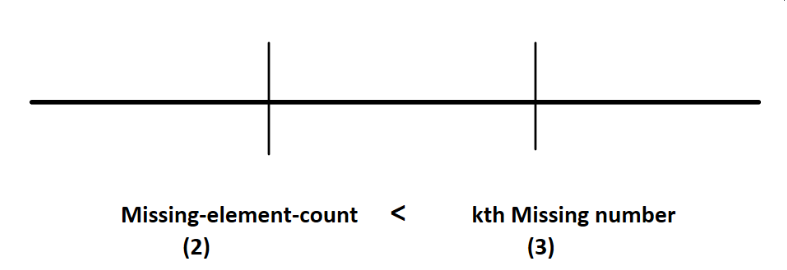
In the above figure kth missing-number is on the right side or we can say K > missing-element–count so, we will increase si =mid+1;
Like the same, if k<= missing-element–count then we move to decrease ei=mid-1;
In this manner, we will narrow our search area while si<=ei
After the end of the loop will find out how many elements are lost in between nums[ei] and the leftmost element

lost=nums[ei]-(leftmost element +ei)

At last, we need to check if there are some elements are missing then we need to make the difference between the kth missing and lost

diff=k-lost

Return nums[ei]+diff

CODE:

JAVA CODE FOR Missing Element in Sorted Array

class Solution {
    public int missingElement(int[] nums, int k) {
        int n=nums.length;
        int leftMost=nums[0];
        int si=0;
        int ei=n-1;
        while(si<=ei){
            int mid=si+(ei-si)/2;
            // missing element in b/w leftmost and nums[mid]
            int missingCount=nums[mid]-(leftMost+mid);
            if(missingCount<k){
                // potential answer on be right side
                si=mid+1;
            }
            else{
                // potential answer on be left side
                ei=mid-1;
            }
            
        }
        // After the end of loop  ei will be on correct position
        // nums[ei] can be our potential answer 
        //lostCount will contain How many elements we lost from leftMost
        int lostCount=nums[ei]-(leftMost+ei);
      // check how much element missed out on ei from leftMost k-lostedCount 
          int diff=k-lostCount;
        // add that diff in nums[ei]
        return nums[ei]+diff;
        
    }
}

C++ CODE FOR Missing Element in Sorted Array

class Solution {
public:
    int missingElement(vector<int>& nums, int k) {
         int n=nums.size();
        int leftMost=nums[0];
        int si=0;
        int ei=n-1;
        while(si<=ei){
            int mid=si+(ei-si)/2;
            // missing element in b/w leftmost and nums[mid]
            int missingCount=nums[mid]-(leftMost+mid);
            if(missingCount<k){
                // potential answer on be right side
                si=mid+1;
            }
            else{
                // potential answer on be left side
                ei=mid-1;
            }
            
        }
        // After the end of loop  ei will be on correct position
        // nums[ei] can be our potential answer 
        //lostCount will contain How many elements we lost from leftMost
        int lostCount=nums[ei]-(leftMost+ei);
         // check how much element missed out on ei from leftMost k-lostedCount 
        int diff=k-lostCount;
        // add that diff in nums[ei]
        return nums[ei]+diff;
    }
};