Arithmetic Slices II – Subsequence LeetCode Solution

Difficulty Level Hard
Frequently asked in Adobe Google Uber
BaiduViews 917

Problem Statement :

Arithmetic Slices II – Subsequence LeetCode Solution – Given an integer array of nums, return the number of all the arithmetic subsequences of nums.

A sequence of numbers is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.

  • For example, [1, 3, 5, 7, 9], [7, 7, 7, 7], and [3, -1, -5, -9] are arithmetic sequences.
  • For example, [1, 1, 2, 5, 7] is not an arithmetic sequence.

A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.

  • For example, [2,5,10] is a subsequence of [1,2,1,2,4,1,5,10].

The test cases are generated so that the answer fits in 32-bit integer.

Example :

Example 1

Input: nums = [2,4,6,8,10]
Output: 7
Explanation: All arithmetic subsequence slices are:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]

Example 2 

Input: nums = [7,7,7,7,7]
Output: 16
Explanation: Any subsequence of this array is arithmetic.

Constraints :

Arithmetic Slices II - Subsequence LeetCode Solution

Observation :

    • To determine an arithmetic sequence, we need at least two parameters: the first element of the sequence, and the common difference.
    • If the first  term of an arithmetic sequence is a1 and the common difference of successive members is d, then the n-th term of the sequence (an) is given by:

                                                                            an = a1 + (n-1)d  

Approach :

  • As we need to find the arithmetic subsequence i.e. elements of an array should be in arithmetic progression no matter they are contiguous or non-contiguous.

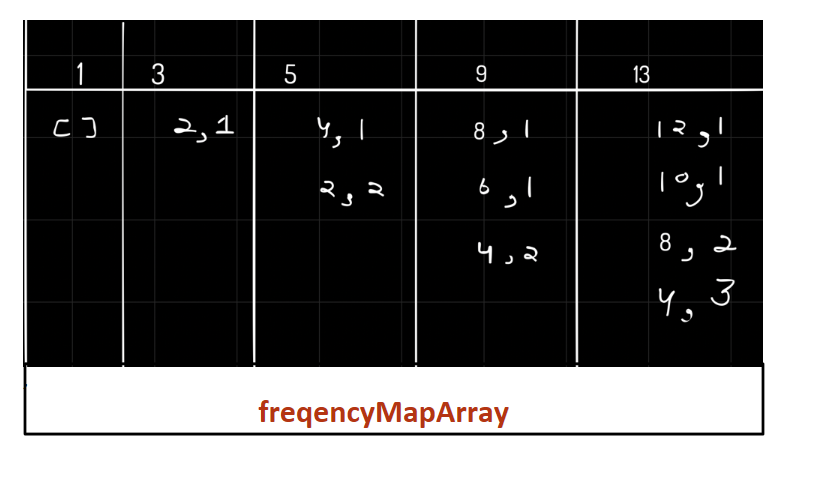
  • We will create an array of maps to store the frequency of difference of an element with respect to its previous elements.

  • In the original definition of arithmetic subsequence, the length of the subsequence must be at least 3. But we are defining new subsequences that are weak subsequences of only length 2.

  • frequencyArrayMap[i] stores the number of weak arithmetic subsequences that end with nums[i] and its common difference is diff.

  • A weak arithmetic sequence has two characteristics that we are defining:

    1.  For any pair i,j (i != j) nums[i] and nums[j] can always form a weak arithmetic subsequence.
    2.  If we add a new element to a weak arithmetic sequence, the new sequence must be an arithmetic sequence, because the new sequence has become the original arithmetic sequence of at least length 3.

  • Now for each nums[i], we will find the nums[j] forming a weak arithmetic sequence of length two.

  • For the nums[j], we will iterate from 0 to less than i.

  • In the FrequencyMapArray, which already stores the common difference of two elements nums[i] and nums[j], if we will find the same common difference for different pairs then we will add that frequency to our answer.

Arithmetic Slices II - Subsequence LeetCode Solution

Code for Arithmetic Slices II – Subsequence :

Java  Code :

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
           int n = nums.length;
        long ans = 0;
        Map<Integer, Integer>[] frequencyArrayMap = new Map[n];
        for(int i=0;i<n;i++){
            frequencyArrayMap[i]=new HashMap<>();
        }
        for(int i=0;i<n;i++){
           for(int  j=0;j<i;j++){
               long commondiff = (long)nums[i]-(long)nums[j];
               if(commondiff<Integer.MIN_VALUE || commondiff> Integer.MAX_VALUE)continue;
               int diff =(int)commondiff;
               int prevFreq=frequencyArrayMap[j].getOrDefault(diff,0);
               int currFreq=frequencyArrayMap[i].getOrDefault(diff,0);
               ans+=prevFreq;
               frequencyArrayMap[i].put(diff,prevFreq+currFreq+1);
           }
        }
        return (int)ans;
        
    }
}

C++ Code :

#define LL long long
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
          int n = nums.size();
        LL ans = 0;
        vector<map<int,int>>frequencyArrayMap(n);
        for(int i=0;i<n;i++){
           for(int  j=0;j<i;j++){
               LL commondiff = (LL)nums[i]-(LL)nums[j];
               if(commondiff<= INT_MIN || commondiff>= INT_MAX)continue;
               int diff =(int)commondiff;
                 int prevFreq =0;
                int currFreq=0;
               
                 if(frequencyArrayMap[j].find(diff) != frequencyArrayMap[j].end()){
                     prevFreq = frequencyArrayMap[j][diff];
                     currFreq = frequencyArrayMap[i][diff];
                    ans += prevFreq;
                      frequencyArrayMap[i][diff] = currFreq + prevFreq + 1; 
                }
                 else{
                    frequencyArrayMap[i][diff]++;
                }
               
          
             
           }
        }
        return (int)ans;
    }
};

Complexity Analysis for Arithmetic Slices II – Subsequence LeetCode Solution:

Time Complexity

O(n2)  , as we are using two loops.

Space Complexity 

O(n2)   For each num [i], we need to store at most n distinct common differences, so the total space complexity is

Translate »