Snakes and Ladders LeetCode Solution

Problem Statement

Snakes and Ladders LeetCode Solution – You are given an n x n integer matrix board where the cells are labeled from 1 to n² in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating directions in each row.

You start on the square 1 of the board. In each move, starting from square curr, do the following:

• Choose a destination square next with a label in the range [curr + 1, min(curr + 6, n²)].
  • This choice simulates the result of a standard 6-sided die roll: i.e., there are always at most 6 destinations, regardless of the size of the board.
• If next has a snake or ladder, you must move to the destination of that snake or ladder. Otherwise, you move to next.
• The game ends when you reach the square n².

A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n² do not have a snake or ladder.

Note that you only take a snake or ladder at most once per move. If the destination of a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.

• For example, suppose the board is [[-1,4],[-1,3]], and on the first move, your destination square is 2. You follow the ladder to square 3, but do not follow the subsequent ladder to 4.

Return the least number of moves required to reach the square n². If it is not possible to reach the square, return -1.

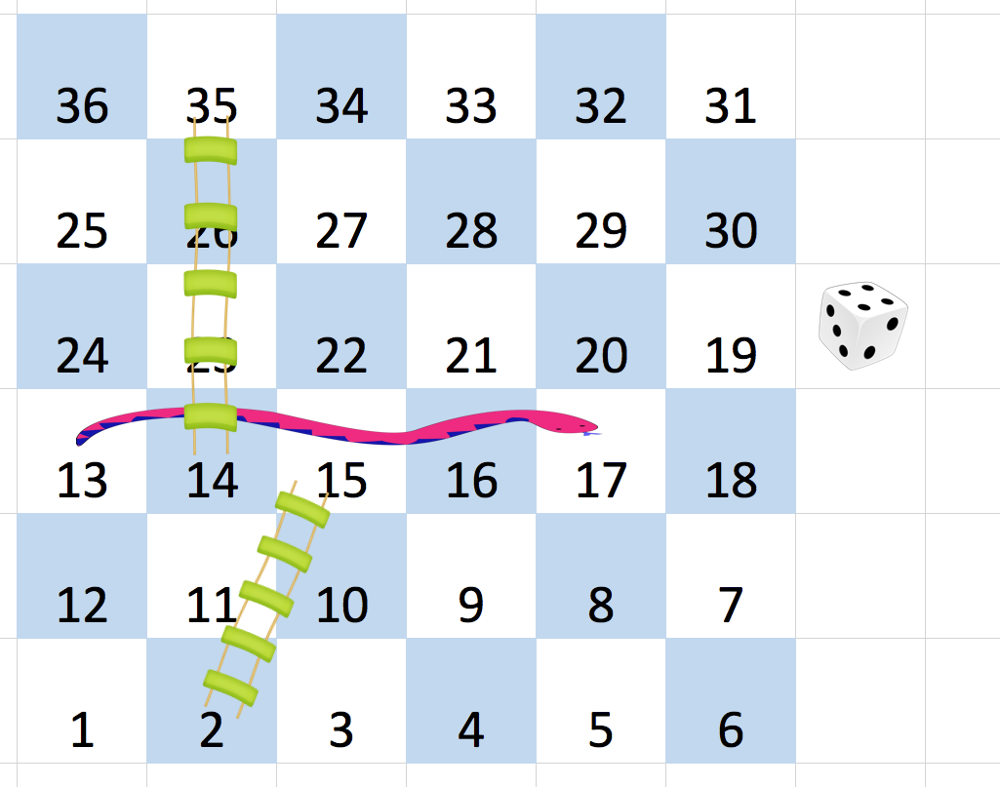
Input: board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
In the beginning, you start at square 1 (at row 5, column 0).
You decide to move to square 2 and must take the ladder to square 15.
You then decide to move to square 17 and must take the snake to square 13.
You then decide to move to square 14 and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
This is the lowest possible number of moves to reach the last square, so return 4.

Explanation

Intuition:
For each step we do the following:

1. roll dice (and check all 6 possible values, marking each as visited)
2. check if we land on a ladder and take it (no possibility to skip it, we must take it)
3. remember where to continue next time (add the new position to the queue)

Now let’s take a look at scenarios:

1. Just step starting from square 1 with a dice where 6 is the best 🙂

Code

C++ Code for Snakes and Ladders

typedef pair<int,int> Pi;
class Solution {
public:
    int snakesAndLadders(vector<vector<int>>& board) {
        int rows=board.size(), cols = board[0].size(), target=rows*cols, r, c, p;
        vector<int> visited(rows*cols + 1); // cells on board start from 1

        // queue contains <priority, square> sorted ascending by priority
        // prio = #steps * 1000 + (500 - square);
        // number of steps is critical and adds 1000; 500 is selected as it is higher than the max cell (20*20=400)
        priority_queue<Pi, vector<Pi>, greater<Pi>> q;
        q.push(make_pair(0,1)); // 0 steps to position 1
        visited[1] = true;

        while(q.size())
        {
            auto step_pos = q.top(); q.pop();
            int s = step_pos.first/1000 + 1;
            
            for(int i=1; i<=6; i++)
            {
                auto p = step_pos.second+i;
                if(visited[p]) continue;
                visited[p] = true;
                
                r = rows - (p-1) / cols - 1;
                c = (p-1) % cols;
                if((rows-r-1)%2) c = cols - c - 1; // change direction for odd lines
                int ladder = board[r][c];
                if(ladder>0 && ladder<=target)
                    p = ladder; // no update for steps. allow to come here again with a dice
                    
                if(p == target) return s;
                q.push(make_pair(s*1000+500-p, p));
            }
        }
        return -1;
    }
};

Python Code for Snakes and Ladders

class Solution:
    def snakesAndLadders(self, board: List[List[int]]) -> int:
        n = len(board)
        def label_to_position(label):
            r, c = divmod(label-1, n)
            if r % 2 == 0:
                return n-1-r, c
            else:
                return n-1-r, n-1-c
            
        seen = set()
        queue = collections.deque()
        queue.append((1, 0))
        while queue:
            label, step = queue.popleft()
            r, c = label_to_position(label)
            if board[r][c] != -1:
                label = board[r][c]
            if label == n*n:
                return step
            for x in range(1, 7):
                new_label = label + x
                if new_label <= n*n and new_label not in seen:
                    seen.add(new_label)
                    queue.append((new_label, step+1))
        return -1

Complexity Analysis for Snakes and Ladders LeetCode Solution

Time Complexity

O(n^2)

Space Complexity

O(n^2)