Table of Contents
Problem Statement
Find the Duplicate Number LeetCode Solution – Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and uses only constant extra space.
Input: nums = [1,3,4,2,2] Output: 2
Explanation
The idea is to reduce the problem to Linked List Cycle II:
Given a linked list, return the node where the cycle begins.
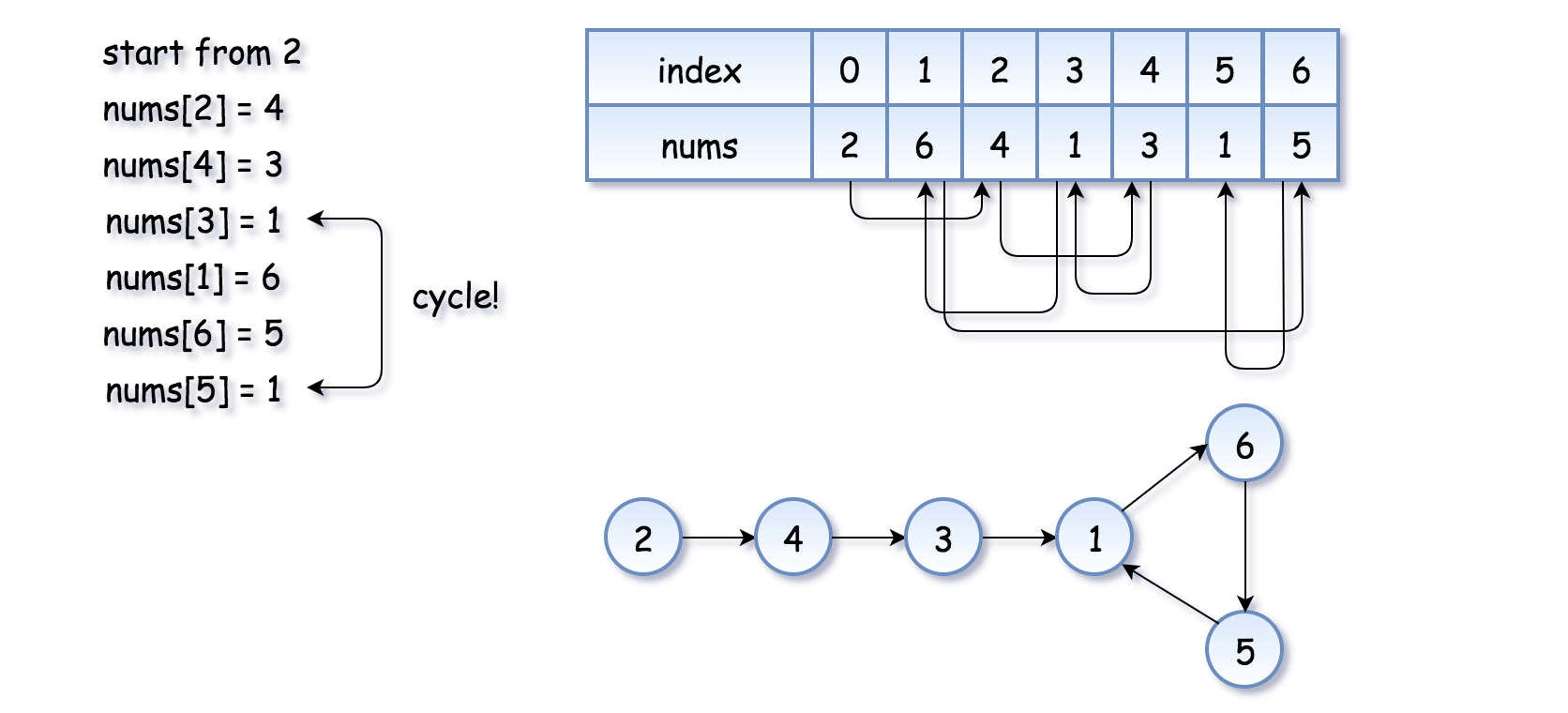
First of all, where does the cycle come from? Let’s use the function f(x) = nums[x] to construct the sequence: x, nums[x], nums[nums[x]], nums[nums[nums[x]]], ....
Each new element in the sequence is an element in nums at the index of the previous element.
If one starts from x = nums[0], such a sequence will produce a linked list with a cycle.
The cycle appears because nums contains duplicates. The duplicate node is a cycle entrance.
Here is how it works:
Algorithm
Floyd’s algorithm consists of two phases and uses two pointers, usually called tortoise and hare.
In phase 1, hare = nums[nums[hare]] is twice as fast as tortoise = nums[tortoise]. Since the hare goes fast, it would be the first to enter the cycle and run around the cycle. At some point, the tortoise enters the cycle as well, and since it’s moving slower the hare catches up to the tortoise at some intersection point. Now phase 1 is over, and the tortoise has lost.
To compute the intersection point, let’s note that the hare has traversed twice as many nodes as the tortoise, i.e. 2d(\text{tortoise}) = d(\text{hare}), implying:
2(F + a) = F + nC + a, where n is some integer.
In phase 2, we give the tortoise a second chance by slowing down the hare, so that it now moves at the speed of the tortoise: tortoise = nums[tortoise], hare = nums[hare]. The tortoise is back at the starting position, and the hare starts from the intersection point.
Let’s show that this time they meet at the cycle entrance after the F steps.
- The tortoise started at zero, so its position after F steps is F.
- The hare started at the intersection point F + a = nC, so its position after F steps is nC + F, which is the same point as F.
- So the tortoise and the (slowed down) hare will meet at the entrance of the cycle.
Code
C++ Code for Find the Duplicate Number
class Solution {
public:
int findDuplicate(vector<int>& nums) {
// Find the intersection point of the two runners.
int tortoise = nums[0];
int hare = nums[0];
do {
tortoise = nums[tortoise];
hare = nums[nums[hare]];
} while (tortoise != hare);
// Find the "entrance" to the cycle.
tortoise = nums[0];
while (tortoise != hare) {
tortoise = nums[tortoise];
hare = nums[hare];
}
return hare;
}
};Java Code for Find the Duplicate Number
class Solution {
public int findDuplicate(int[] nums) {
// Find the intersection point of the two runners.
int tortoise = nums[0];
int hare = nums[0];
do {
tortoise = nums[tortoise];
hare = nums[nums[hare]];
} while (tortoise != hare);
// Find the "entrance" to the cycle.
tortoise = nums[0];
while (tortoise != hare) {
tortoise = nums[tortoise];
hare = nums[hare];
}
return hare;
}
}Python Code for Find the Duplicate Number
class Solution:
def findDuplicate(self, nums):
# Find the intersection point of the two runners.
tortoise = hare = nums[0]
while True:
tortoise = nums[tortoise]
hare = nums[nums[hare]]
if tortoise == hare:
break
# Find the "entrance" to the cycle.
tortoise = nums[0]
while tortoise != hare:
tortoise = nums[tortoise]
hare = nums[hare]
return hareComplexity Analysis for Find the Duplicate Number LeetCode Solution
Time Complexity
O(n)
Space Complexity
O(1)