Parallel Courses II LeetCode Solution

Problem Statement

Parallel Courses II LeetCode Solution- You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCourse_i, nextCourse_i], representing a prerequisite relationship between course prevCourse_i and course nextCourse_i: course prevCourse_i have to be taken before the course nextCourse_i. Also, you are given the integer k.

In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return the minimum number of semesters needed to take all courses. The test cases will be generated such that it is possible to take every course.

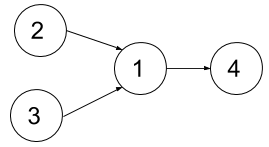
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2
Output: 3 
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 2 and 3.
In the second semester, you can take course 1.
In the third semester, you can take course 4.

Explanation

Let us denote by dp[i][j] tuple with:

1. minimum number of days we need to finish
2. number of non-zero bits for the binary mask of the last semester
3. binary mask of the last semester

all courses denoted by the binary mask i and such that the last course we take is j. For example for dp[13][3], i=13 is represented as 1101, and it means that we take courses number 0, 2, 3 and the last one we take is the number 3. (instead of starting with 1, let us subtract 1 from all courses and start from 0).

Let us also introduce bm_dep[i]: this will be a binary mask for all courses we need to take before we can take course number i. For example bm_dep[3] = 6 = 110 means, that we need to take courses 1 and 2 before we can take the course number 3.

Now, let us iterate overall i in range(1<<n). Let us evaluate, n_z_bit this will be an array with all places with non-zero bits. For example for i=13=1101, n_z_bit = [0,2,3].

What we need to do next :

1. First, check that we really can take a new course number j, using bm_dep[j] & i == bm_dep[j].
2. Now, we want to update dp[i][j], using dp[i^(1<<j)][t], for example, if we want to find answers for (1,3,4,5) courses with 3 being the last course, it means that we need to look into (1,4,5) courses, where we add a course 3.
3. We check how many courses we already take in the last semester, using, and also make sure, that we can add a new course to the last semester. Now we have two candidates: (cand, bits + 1, mask + (1<<j)) and dp[i][j] and we need to choose the best one. In another case, we need to take a new semester: so cands will be equal to cands + 1, bits will be equal to 1 and binary mask for last semester is 1<<j.

Code

Java Code for Parallel Courses II

class Solution {
    public int minNumberOfSemesters(int n, int[][] relations, int k) {
        int[] prereq = new int[n];
        for (int[] req : relations) {
            prereq[req[1] - 1] |= 1 << (req[0] - 1);
        }
        int[] dp = new int[(1 << n)];
        Arrays.fill(dp, -1);
        return solve(0, n, k, prereq, dp);
    }

    private int solve(int mask, int n, int k, int[] prereq, int[] dp) {
        if (mask == (1 << n) - 1) {
            return 0;
        }
        if (dp[mask] != -1) {
            return dp[mask];
        }
        int availableCourses = 0;
        for (int i = 0; i < n; i += 1) {
            if ((mask & prereq[i]) == prereq[i]) {
                if( (mask & (1<<i))>0 )
                    continue;
                availableCourses |= 1 << i;
            }
        }
        int best = Integer.MAX_VALUE / 2;
        for (int submask = availableCourses; submask > 0; submask = (submask - 1) & availableCourses) {
            if (Integer.bitCount(submask) <= k) {
                best = Math.min(best, 1 + solve(mask | submask, n, k, prereq, dp));
            }
        }
        return dp[mask] = best;
    }
}

Python Code for Parallel Courses II

class Solution:
    def minNumberOfSemesters(self, n: int, relations: List[List[int]], k: int) -> int:
        self.degree = [0] * n
        memo = collections.defaultdict(list)
        for i,j in relations:
            memo[i - 1] += j - 1,
            self.degree[j - 1] += 1
        @lru_cache(None)
        def solve(mask):
            if mask == (1 << n) - 1: 
                return 0
            take = []
            for i in range(n):
                if not mask & 1 << i and self.degree[i] == 0:
                    take += i,
            ans = float('inf')
            for i in combinations(take, min(k, len(take))):
                temp = mask
                for j in i:
                    temp |= 1 << j
                    for a in memo[j]:
                        self.degree[a] -= 1
                ans = min(ans, 1 + solve(temp))
                for j in i:
                    for a in memo[j]:
                        self.degree[a] += 1
            return ans
        return solve(0)

Complexity Analysis for Parallel Courses II LeetCode Solution

Time Complexity

O(3^n)

Space Complexity

O(n)