Consider a sorted array but one index was picked and the array was rotated at that point. Now, once the array has been rotated you are required to find a particular target element and return its index. In case, the element is not present, return -1. The problem is generally referred to as Search in Rotated Sorted Array Leetcode Solution. So in the question, we are provided with an array of some integer elements that are sorted and rotated at a certain index that is not known to us. Along with the array, we are also given a specific element that we need to find.
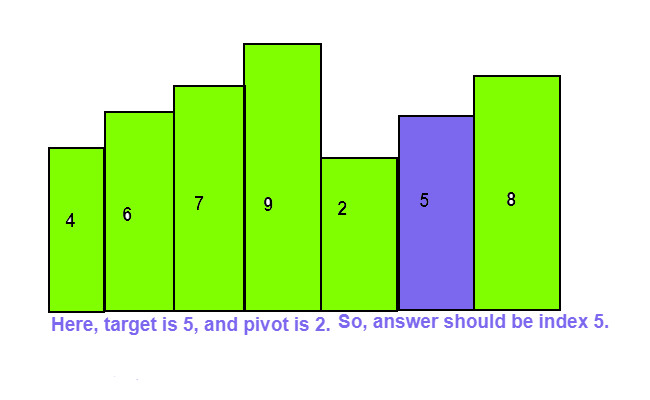
array: [4,5,6,7,0,1,2] target: 4
0
Explanation: Since the element to be searched is 4. The element is found at index 0, we return the index of the target.
array: [4,5,6,7,0,1,2] target: 3
-1
Explanation: Since the element is not present in the array, we return -1.
Table of Contents
Brute Force Approach for Search in Rotated Sorted Array
The problem “Search in Rotated Sorted Array” asks us to find the index of the target element in the given rotated sorted array. And we have already discussed what a rotated sorted array is? So, the simplest method that one can think of is to try Linear Search. In Linear Search, we simply traverse the given array and check if the current element is our target element. If the current element is the target element we return the current index else we return -1. The approach is very simple but since it does not uses the fact that the array is sorted and rotated at a single index. This approach has linear time complexity.
Code for Search in Rotated Sorted Array Leetcode Solution
C++ code
#include <bits/stdc++.h>
using namespace std;
int search(vector<int>& nums, int target) {
int n = nums.size();
for(int i=0;i<n;i++)
if(nums[i] == target)
return i;
return -1;
}
int main(){
vector<int> nums({4,5,6,7,0,1,2});
cout<<search(nums, 4);
}
0
Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
public static int search(int[] nums, int target) {
int n = nums.length;
for(int i=0;i<n;i++)
if(nums[i] == target)
return i;
return -1;
}
public static void main(String[] args){
int nums[] = {4,5,6,7,0,1,2};
System.out.println(search(nums, 4));
}
}0
Complexity Analysis
Time Complexity
O(N), because in the worst case, the target element may be present at the end of the array. Thus the time complexity is linear.
Space Complexity
O(1), since we do not any information regarding each element specifically and have used a constant number of variables. Thus the space complexity is constant.
Optimized Approach for Search in Rotated Sorted Array
The approach earlier mentioned did not use the fact that the array was a rotated sorted array. So, in this approach, we try to use this fact to reduce the time complexity. Consider, if we had a sorted array, we would have simply used binary search but in case this is a bit tricky. Here also we are required to used binary search. But if we use binary search, how do we get to know which part of the array to choose once we are at the middle element of the array? Because we cannot simply follow the original binary search algorithm because this is a rotated sorted array. So, there is a slight modification over the normal binary search.
So, typically in a binary search, we check if the current element(element at mid index) is same as target, then we return its index. This step remains same here. Other than that, if they are not same, we check if the pivot lies to the right [of the current element or to the left. If it lies to the right, then we check if the target lies in non-rotated subarray, if it does we update the high else we update the low. Similarly, if the pivot lies to the left, again we check if the target lies in the non-rotated subarray, we update the low, else we update the high. And in the end, if we come out of the loop, we are sure that the target is not present in the given array.
Optimized code for Search in Rotated Sorted Array Leetcode Solution
C++ code
#include <bits/stdc++.h>
using namespace std;
int search(vector<int>& nums, int target) {
int n = nums.size();
int low = 0, high = n-1;
while(low<=high){
int mid = (low+high)/2;
// check if the current element is target
if(nums[mid] == target)
return mid;
// if the starting index of the search space has smaller element than current element
else if(nums[low]<=nums[mid]){
// if target lies in non-rotated search space (or subarray)
if(target >= nums[low] && target < nums[mid])
high = mid - 1;
else
low = mid + 1;
} else {
// if target lies in non-rotated subarray
if(target>nums[mid] && target<=nums[high])
low = mid + 1;
else
high = mid - 1;
}
}
// if you couldn't find the target element until now then it does not exists
return -1;
}
int main(){
vector<int> nums({4,5,6,7,0,1,2});
cout<<search(nums, 4);
}
0
Java code
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
public static int search(int[] nums, int target) {
int n = nums.length;
int low = 0, high = n-1;
while(low<=high){
int mid = (low+high)/2;
// check if the current element is target
if(nums[mid] == target)
return mid;
// if the starting index of the search space has smaller element than current element
else if(nums[low]<=nums[mid]){
// if target lies in non-rotated search space (or subarray)
if(target >= nums[low] && target < nums[mid])
high = mid - 1;
else
low = mid + 1;
} else {
// if target lies in non-rotated subarray
if(target>nums[mid] && target<=nums[high])
low = mid + 1;
else
high = mid - 1;
}
}
// if you couldn't find the target element until now then it does not exists
return -1;
}
public static void main(String[] args){
int nums[] = {4,5,6,7,0,1,2};
System.out.println(search(nums, 4));
}
}0
Complexity Analysis
Time Complexity
O(log N), since we have used binary search to find the target element. The time complexity is logarithmic.
Space Complexity
O(1), since we stored only some constant number of elements, the space complexity is constant.