In the problem “Find the smallest range containing elements from k lists” we have given K lists which are sorted and of the same size N. It asks to determine the smallest range that contains at least element(s) from each of the K lists. If there is more than one smallest range present, then print any of the range.
Table of Contents
Example
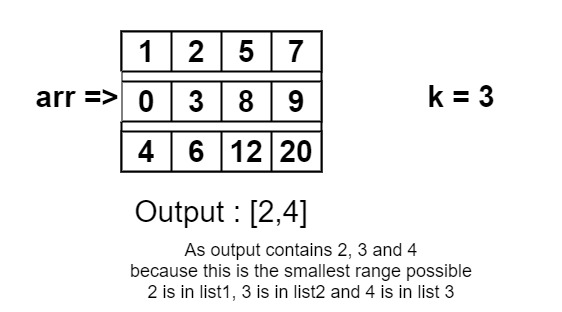
arr[][] = { {1, 2, 5, 7 }, {0, 3, 8, 9 }, {4, 6, 12,20 } }2 4
Explanation: From 2 in 1st list and 4 in the 3rd list, we have 3 from 2nd list, so within 2 and 4 in range, we have at least elements from each list.
arr[][] = { {2, 8, 9, 20}, {6, 7, 10, 11}, {3, 14, 30, 39} };2 6
Explanation: From 2 in 1st list and 6 in 2nd list we have 3 from 3rd list, so within 2 and 6 in range, we have at least element from each list.
Algorithm to find smallest range containing elements from k lists
1. Create a Heap( Min Heap Data Structure). 2. Store k elements into it picking one from each array. 3. Declare a variable min and a range and set to a maximum value of an Integer and a variable max to the maximum value of an Integer. 4. Keep storing each element from every list and find the maximum value and store it into a max variable we declared. 5. Using a root variable or any object of a Min Heap, start to find the minimum element and store it to min. 6. Find the minimum range by checking if the current (maximum − minimum ) is less than the min, range and update the range. 7. Remove the current root element or top from the used data structure and pick the next element and insert it, from the list 8. The list that contains the minimum element, chose that. 9. Find the max element and update it according to the new element that was inserted.
Explanation
We have given a k sorted lists, for that we have to find the smallest range and also within that range, at least element(s) number should be present from each list. Use a Min Heap data structure and its characteristics. We made a root or top pointer to indicate the current element or top element just to remove or insert.
We will first find the maximum element from all of the lists, once we have found the maximum element we will store it to the max. The idea is to find the maximum from the 0th index from all of the lists. Suppose we have three lists, now picking up the first element of all of the lists. We will compare it among all of them, and find out the maximum of all. This is just to make sure that we get the smallest range. Because we know we can start from the 0th indexes from all of the lists, but to reduce the range to become the smallest, we will also push the starting index.
Basically, after finding out the maximum element, we will be building a min Heap. Heapify function does that for us too. Now Min Heap does the work as it builds the type of array to store minimum elements first and arrange the number in increasing order through building a Heap. So this function does the same for us. But we have to find the smallest range, although we found one. We have to make sure to be the smallest range so it might be possible, that, we can update it.
We will be swapping up the values, and in getMin function, we will be getting our smallest element. Then we will be updating the range value. We have to find the start and end of that range, minimum to start, and maximum to end and will be printing that element.
Implementation
C++ program to find smallest range containing elements from k lists
#include<bits/stdc++.h>
using namespace std;
#define N 5
struct Node
{
int element;
int i;
int j;
};
void swap(Node* x, Node* y);
class MinHeap
{
Node* heapArray;
int heap_size;
public:
MinHeap(Node a[], int size);
void MinHeapify(int);
int left(int i)
{
return (2 * i + 1);
}
int right(int i)
{
return (2 * i + 2);
}
Node getMin()
{
return heapArray[0];
}
void replaceMin(Node x)
{
heapArray[0] = x;
MinHeapify(0);
}
};
MinHeap::MinHeap(Node a[], int size)
{
heap_size = size;
heapArray = a;
int index = (heap_size - 1) / 2;
while (index >= 0)
{
MinHeapify(index);
index--;
}
}
void MinHeap::MinHeapify(int i)
{
int l = left(i);
int r = right(i);
int smallest = i;
if (l < heap_size && heapArray[l].element < heapArray[i].element)
smallest = l;
if (r < heap_size && heapArray[r].element < heapArray[smallest].element)
smallest = r;
if (smallest != i)
{
swap(heapArray[i], heapArray[smallest]);
MinHeapify(smallest);
}
}
void getSmallestRangeKElements(int arr[][N], int k)
{
int range = INT_MAX;
int min = INT_MAX, max = INT_MIN;
int start, end;
Node* heapArray = new Node[k];
for (int i = 0; i < k; i++)
{
heapArray[i].element = arr[i][0];
heapArray[i].i = i;
heapArray[i].j = 1;
if (heapArray[i].element > max)
max = heapArray[i].element;
}
MinHeap MinHeapObj(heapArray, k);
while (1)
{
Node root = MinHeapObj.getMin();
min = MinHeapObj.getMin().element;
if (range > max - min + 1)
{
range = max - min + 1;
start = min;
end = max;
}
if (root.j < N)
{
root.element = arr[root.i][root.j];
root.j += 1;
if (root.element > max)
max = root.element;
}
else
break;
MinHeapObj.replaceMin(root);
}
cout << "Smallest range: "<< "["<< start << " " << end << "]";
}
int main()
{
int arr[][N] = {{1, 2, 5, 7 },
{0, 3, 8, 9 },
{4, 6, 12,20 }
};
int k = sizeof(arr) / sizeof(arr[0]);
getSmallestRangeKElements(arr, k);
return 0;
}
Smallest range: [2 4]
Java program to find smallest range containing elements from k lists
class smallestRange
{
public static class Node
{
int element;
int i;
int j;
Node(int a, int b, int c)
{
this.element = a;
this.i = b;
this.j = c;
}
}
public static class MinHeap
{
Node[] heapArray;
int size;
MinHeap(Node[] arr, int size)
{
this.heapArray = arr;
this.size = size;
int i = (size - 1) / 2;
while (i >= 0)
{
MinHeapify(i);
i--;
}
}
int left(int i)
{
return 2 * i + 1;
}
int right(int i)
{
return 2 * i + 2;
}
void MinHeapify(int i)
{
int l = left(i);
int r = right(i);
int small = i;
if (l < size && heapArray[l].element < heapArray[i].element)
small = l;
if (r < size && heapArray[r].element < heapArray[small].element)
small = r;
if (small != i)
{
swap(small, i);
MinHeapify(small);
}
}
void swap(int i, int j)
{
Node temp = heapArray[i];
heapArray[i] = heapArray[j];
heapArray[j] = temp;
}
Node getMinimum()
{
return heapArray[0];
}
void replaceMin(Node x)
{
heapArray[0] = x;
MinHeapify(0);
}
}
public static void getSmallestRangeKElements(int[][] arr, int k)
{
int range = Integer.MAX_VALUE;
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
int start = -1, end = -1;
int n = arr[0].length;
Node[] arr1 = new Node[k];
for (int i = 0; i < k; i++)
{
Node node = new Node(arr[i][0], i, 1);
arr1[i] = node;
max = Math.max(max, node.element);
}
MinHeap MinHeapObj = new MinHeap(arr1, k);
while (true)
{
Node root = MinHeapObj.getMinimum();
min = root.element;
if (range > max - min + 1)
{
range = max - min + 1;
start = min;
end = max;
}
if (root.j < n)
{
root.element = arr[root.i][root.j];
root.j++;
if (root.element > max)
max = root.element;
}
else
break;
MinHeapObj.replaceMin(root);
}
System.out.println("Smallest range: [" + start + " " + end + "]");
}
public static void main(String[] args)
{
int arr[][] = { {1, 2, 5, 7 },
{0, 3, 8, 9 },
{4, 6, 12,20 }
};
int k = arr.length;
getSmallestRangeKElements(arr, k);
}
}
Smallest range: [2 4]
Complexity Analysis
Time Complexity
O(n * k *log k) where “k” is the length of min-heap and “n” is the length of each array.
Space Complexity
O(k) where “k” is the length of priority queue which will store elements.