Construct Binary Tree from Preorder and Postorder Traversal LeetCode Solution

Problem Statement

Construct Binary Tree from Preorder and Postorder Traversal LeetCode Solution – Given two integer arrays, preorder and postorder where preorder is the preorder traversal of a binary tree of distinct values and postorder is the postorder traversal of the same tree, reconstruct and return the binary tree.

If there exist multiple answers, you can return any of them.

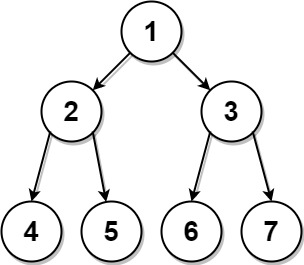
Input: preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
Output: [1,2,3,4,5,6,7]

Explanation

We know that the first element in the pre array is the root. We also know that the second element in the pre array is the root of the left subtree. Now if we can find this second element in the post array then all elements before it and including it would belong to the left subtree and all elements after it (excluding the last element which is the root) will be the elements in the right subtree. We can apply this logic recursively while processing each element in the pre array and building the tree. We use a hashmap for fast lookups in the post array.

The problem is easier to solve if we decrease it into subproblems using Divide and Conquer.

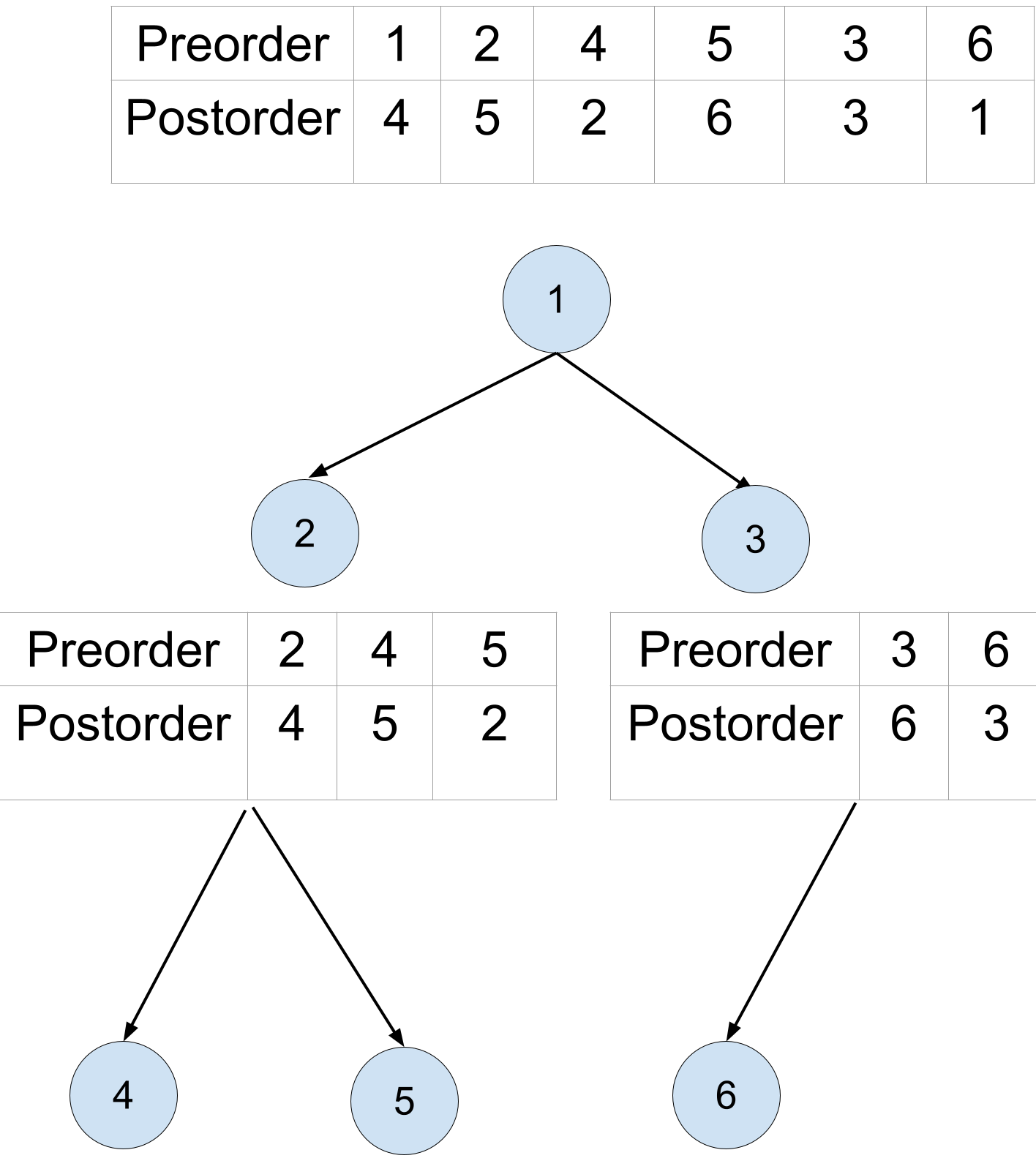
Given preorder : 1 2 4 5 3 6 and postorder : 4 5 2 6 3 1

We can se it as : 1 ( 2 4 5) ( 3 6 ) and ( 4 5 2 ) ( 6 3 ) 1

Code

C++ Code For Construct Binary tree from preorder and postorder traversal

#define null nullptr
class Solution {
public:
    int i = 0;
    TreeNode* help(vector<int>& pre, vector<int>& post,int start,int end){
        //BAse Case
        if(start>end) return null;
        if(i>=pre.size()) return null;
        int j =-1;
        for(int k = start;k<=end;k++)
            if(pre[i]==post[k]){
                j=k;
                break;
            }
        if(j==-1) return null;
        i++;
        TreeNode* root = new TreeNode(post[j]);
        TreeNode* l = help(pre,post,start,j-1);
        root->left=l;
        TreeNode* r = help(pre,post,start,j-1);
        root->right=r;
        return root;
    }
    TreeNode* constructFromPrePost(vector<int>& pre, vector<int>& post) {
        return help(pre,post,0,post.size()-1);
    }
};

Python Code For Construct Binary tree from preorder and postorder traversal

class Solution:
    def constructFromPrePost(self, pre, post):
        return self.constructFromPrePostRecurUtil(
            pre, 0, len(pre) - 1, post, 0, len(post) - 1)
        
    def constructFromPrePostRecurUtil(
            self, 
            pre, 
            preStart, 
            preEnd, 
            post, 
            postStart, 
            postEnd):
        # Base case.
        if (preStart > preEnd):
            return None
        if (preStart == preEnd):
            return TreeNode(pre[preStart])
        # Recursive case.
        root = TreeNode(pre[preStart])
        leftRootIndexInPre = preStart + 1
        leftRootIndexInPost = self.getIndexInPost(
            post, pre[leftRootIndexInPre])
        leftEndIndexInPre = leftRootIndexInPre + \
            (leftRootIndexInPost - postStart)
        root.left = self.constructFromPrePostRecurUtil(
            pre, 
            leftRootIndexInPre, 
            leftEndIndexInPre, 
            post, 
            postStart, 
            leftRootIndexInPost)
        root.right = self.constructFromPrePostRecurUtil(
            pre, 
            leftEndIndexInPre + 1, 
            preEnd, 
            post, 
            leftRootIndexInPost + 1, 
            postEnd - 1)
        return root
        
    def getIndexInPost(self, post, target):
        for i, v in enumerate(post):
            if v == target:
                return i
        return -1   # to optimize

Java Code For Construct Binary tree from preorder and postorder traversal

class Solution {
    public TreeNode helper(int[] pre,int[] post,int psi,int pei,int ppsi,int ppei ) {
        if (psi>pei) return null;
        TreeNode root=new TreeNode(pre[psi]);
        if(psi==pei) return root;
        int idx=ppsi;
        while(post[idx]!=pre[psi+1]){idx++;}
        int tne=idx-ppsi+1;
        root.left=helper(pre,post,psi+1,psi+tne,ppsi,idx);
        root.right=helper(pre,post,psi+tne+1,pei,idx+1,ppei-1);
        return root;
    }
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        return helper(preorder,postorder,0,preorder.length-1,0,postorder.length-1);
    }
}

Complexity Analysis for Construct Binary Tree from Preorder and Postorder Traversal LeetCode Solution

Time Complexity

O(nlogn)

Space Complexity

O(1)