Determine Whether Matrix Can Be Obtained By Rotation LeetCode Solution

Problem Statement

Determine Whether Matrix Can Be Obtained By Rotation LeetCode Solution – Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.

Examples

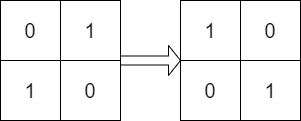
Input:

 mat = [[0,1],[1,0]], target = [[1,0],[0,1]]

Output:

 true

Explanation:

We can rotate mat 90 degrees clockwise to make mat equal target.

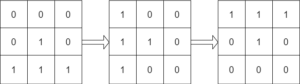
Input:

 mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]

Output:

 true

Explanation:

We can rotate mat 90 degrees clockwise two times to make mat equal target.

Approach

Brute Force Approach

The first approach that comes to mind, is to rotate the matrix and compare it with the target matrix whether they are equal or not, We can repeat the above process 4 times as after 4 times the matrix will repeat itself. The time complexity for this approach is O(4*n*n). Here we are traversing the matrix 4 times to rotate it, Can it be done using only a single traversal, Let’s see!

Optimal Approach

We can do this in a single traversal, In a single traversal, we can compare all the four rotations possible, unlike the above approach in which we are traversing the matrix 4 times.

Conditions for four rotations:

1. matrix[i][j] = target[i][j], if given matrix is equal to target.
2. matrix[i][j] = target[j][n-1-i] , if the given matrix is rotated clckwise , 1 time.
3. matrix[i][j] = target[n-1-i][n-1-j] , if given matrix is rotated clockwise , 2 times.
4. matrix[i][j] = target[n-1-j][i] , it the given matrix is rotated clockwise , 3 times.

If we check the above 4 conditions in one traversal, then we have checked all the possible rotations, if any of them is true means a target is possible.

Let’s see the code for a better understanding.

Code for Determine Whether Matrix Can Be Obtained By Rotation

C++ Code

class Solution {
public:
    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        bool p=true,q=true,r=true,s=true;
        // four variables to check whether target is any rotation of matrix or not.
        
        int n = mat.size();
        int m = mat[0].size();
        
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(mat[i][j]!=target[i][j]){p=false;}
                if(mat[i][j]!=target[n-j-1][i]){q=false;}
                if(mat[i][j]!=target[n-1-i][n-1-j]){r=false;}
                if(mat[i][j]!=target[j][n-1-i]){s=false;}
            }
        }
        
        return p|q|r|s;
        //if any of them is true , means we have find one rotation which equals target.
    }
};

Java Code

class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        boolean p=true,q=true,r=true,s=true;
        // four variables to check whether target is any rotation of matrix or not.
        
        int n = mat.length;
        int m = mat[0].length;
        
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(mat[i][j]!=target[i][j]){p=false;}
                if(mat[i][j]!=target[n-j-1][i]){q=false;}
                if(mat[i][j]!=target[n-1-i][n-1-j]){r=false;}
                if(mat[i][j]!=target[j][n-1-i]){s=false;}
            }
        }
        
        return p|q|r|s;
        //if any of them is true , means we have find one rotation which equals target.
    }
}

Complexity Analysis for Determine Whether Matrix Can Be Obtained By Rotation LeetCode Solution

Time Complexity

Since We are traversing the matrix only once,  the time complexity is O(n*n), where n*n is the size of the given matrix.

Space Complexity

We are only using four variables, So the space complexity is O(1).